The current methods for evaluating the stability of cast-in-place pile hole walls are inefficient and have poor accuracy, leading to incorrect selection of steel reinforcement methods and affecting the quality of construction projects. To address the above issues, a smart evaluation method for the stability of cast-in-place pile hole walls is proposed, taking the southeastern coastal region as an example. Firstly, a wall stability evaluation index system was constructed based on typical local geological conditions, covering dimensions such as geological factors, groundwater levels, and construction parameters. Principal Component Analysis (PCA) and Factor Analysis (FA) were applied to extract key feature variables. Secondly, historical data from 90 CIPP engineering projects were preprocessed through cleaning and normalization, and then divided into training and testing sets in a 7:3 ratio. A multi-strategy Harris Hawks Optimization (MHHO) algorithm was used to optimize the initial weights of the Backpropagation Neural Network (BPNN), thereby building a stability prediction model. Finally, the model performance was evaluated using multiple metrics including F1-score, AUC, recall, and fitting degree. The results show that MHHO-BPNN achieved an accuracy of 0.967 and an F1-score of 0.975 on the test set, significantly outperforming mainstream benchmark models such as the Genetic Algorithm-optimized BPNN (RGA-BPNN) and the Particle Swarm Optimization-based SVM (IPSO-SVM). This method provides data support for rapid evaluation of wall stability and reinforcement scheme formulation, and demonstrates strong potential for practical engineering applications.

Keywords: Cast-in-place pile, Stability evaluation, Southeast coastal areas, BPNN, Harris Eagle optimization algorithm

The research on the stability evaluation of the borehole wall of Cast-in-Place Piles (CIPPs) is an important issue in engineering construction, which can provide data support for the formulation and selection of reinforcement strategies for CIPPs. Therefore, it is directly related to the construction quality and safety of pile foundations. The CIPP hole wall stability refers to the bottom hole wall stability of the pile hole during the drilling process. It is influenced by multiple factors such as geological conditions, engineering loads, and material strength. If the hole wall is unstable, it will lead to pile foundation engineering accidents, seriously affecting the construction progress and quality [1, 2]. The traditional evaluation method for the stability of CIPP hole walls usually uses on-site monitoring, geological exploration, and other means, and then evaluates it through manual processing and analysis of data. For the ellipticity defect in CIPP, VanHorn an improved analytical solution to calculate the critical flexion pressure of the ellipticity imperfect lining with annular gap influence. The results showed that the new method was in good agreement with the experimental data, which could effectively predict the flexion pressure of the lining [3]. However, these methods have problems such as long cycles, high costs, and strong subjectivity. Therefore, finding a more accurate and efficient evaluation method is crucial. Based on this, the hole wall of CIPP has been reinforced. This improves the quality and safety of pile foundation engineering, while also saving costs and shortening the construction period for the project. The study takes the southeastern coastal area as an example to explore the intelligent and high-precision evaluation approach for the borehole wall stability of CIPPs. Back-propagation Neural Network (BPNN) is a mature artificial intelligence technology that has been widely applied in intelligent evaluation, intelligent prediction, and feature classification. The BPNN is used for intelligent evaluation of CIPP pore wall stability to improve the objectivity and accuracy. However, the BPNN model has significant shortcomings. Its performance heavily depends on the initial parameter selection [4, 5]. To address this issue, a Multiple Strategy-Harris Hawks Optimization (MHHO) algorithm is proposed to optimize BPNN. By obtaining the optimal initial parameters, the performance and evaluation accuracy can be improved. The main innovations of the study are twofold. The first is to utilize the BPNN model to achieve intelligent and efficient evaluation of the CIPP hole wall. The second is to propose a HHO based on multi-strategy optimization. MHHO is applied to optimize the BPNN and improve the evaluation accuracy.
It is expected to improve the traditional CIPP hole wall stability evaluation method by introducing intelligent algorithms and optimization techniques, providing more accurate and efficient evaluation tools for the engineering and construction industries. This will not only help to improve the quality and safety of pile foundation construction, but also promote the technological progress and innovative development of the engineering construction industry. The main structure includes four parts. The first part is to organize and analyze the current research on CIPPs and BPNN. The second part is to construct an intelligent evaluation model for the stability of CIPP hole walls based on MHHO-BPNN. The third part is to analyze the performance of the CIPP hole wall stability intelligent evaluation model. The last part is a summary of the research content.
Related works
In the southeastern coastal areas of China, due to the unique geographical location, the local area is mainly composed of soft soil with abundant water. The soil bearing capacity is relatively weak, making it difficult to meet the construction needs of modern construction projects. In this context, the CIPPs is applied to reinforce the foundation and improve the bearing capacity, which can enhance the safety and quality of construction projects. It is crucial for the economic growth of the southeastern coastal areas. Therefore, CIPPs have received attention from different researchers. Shi R et al. conducted experiments in a permafrost region to investigate the effect of freeze-thaw cycles on the CIPPs. It had reference significance for the construction projects in permafrost areas [6]. The soil bearing capacity of coral sand was weak, making it difficult to meet the construction needs. Therefore, Ding X et al. used CIPPs to reinforce the soil. On this basis, the bearing performance of the CIPP under vertical load was analyzed, providing data support for the construction of coral sand soil engineering [7]. In response to the lack of a unified and efficient calculation method for the thermal resistance of parallel U-shaped grouting energy piles, Park S et al. proposed an empirical formula for the thermal resistance of parallel U-shaped grouting energy piles. The calculation efficiency and accuracy of drilling thermal resistance were improved, providing theoretical and data support for the application of parallel U-shaped CIPPs [8]. A’amal A et al. analyzed the performance of defective CIPPs by testing defective model piles in soil. The model pile test results were discussed from a geotechnical engineering project or structural perspective based on the type of failure, providing data support for the repair of defective CIPPs [9]. For large-scale projects with a large amount of mud at the bottom of CIPP, Heo designed a bidirectional load test to explore the effect of mud on the CIPPs. Numerical analysis showed that the slurry was easily mixed with the poured concrete. Therefore, general mud not have a significant impact on the CIPPs [10]. In response to the special geographical environment in plateau areas and the low applicability of pre-stressed CIPPs for general structures, Huang et al. designed a CIPP for plateau areas. This method was applied to transmission line engineering in plateau areas. According to the findings, the CIPP had good application effects [11]. Liu et al. constructed a theoretical way for heat transfer and temperature characteristics based on the surrounding environment and the physical characteristics of the CIPP itself. Thus, the heat conduction process of CIPPs was studied. The integrity of the CIPP was tested, providing theoretical guidance for the research of CIPPs [12]. Yamany M S et al. designed a probability model. It was applied to predict the overall structural of CIPPs and analyze the degradation of highway tunnels. This method provided data support for tunnel engineering maintenance, improving the economy and safety of tunnel engineering maintenance work [13].
BPNN is a neural network that has extensive future and excellent performance. It has broad application value in fields such as intelligent evaluation, prediction, and feature classification. Chen L et al. constructed an evaluation model for university research performance management using an improved BPNN. It achieved scientific, intelligent, and high-precision evaluation of scientific research performance management, providing data support for optimizing scientific research performance management [14]. Li et al. constructed an intelligent urban building information model based on improved BPNN for evaluating and managing urban intelligent buildings, promoting the modernization and intelligent development of cities [15]. Wu et al. proposed an improved Simulated Annealing algorithm (SA) based on Genetic Algorithm (GA). Then, based on the improved SA, the structure of BPNN was optimized to improve the performance. This study provided new ideas and theoretical references for the performance optimization and application of BPNN [16]. Tang et al. proposed an improved BPNN model for fitting, training, and learning color fundi images. The trained BPNN model was used for retinal vascular segmentation to improve the efficiency and accuracy of retinal vascular segmentation, enhancing treatment effectiveness [17]. Liu et al. designed a three-layer training BPNN model. This model realized the intelligent prediction of cross network society relations, reduced the complexity of this work, and improved the efficiency of social relations prediction. The findings demonstrated that it had high prediction accuracy [18]. Wang L et al. used the GA for global optimization to acquire the optimal initial parameters. The enhanced BPNN was used to intelligently and efficiently evaluate the risks of knowledge fusion in the innovation ecosystem, providing data support for knowledge fusion in the innovation ecosystem [19]. Zhang et al. explored the application path and effectiveness of BPNN in the financial field. A stock price pattern classification and prediction model was constructed based on BPNN. After testing, the classification and prediction accuracy of the model exceeded 90%, indicating good performance [20]. Li et al. built a comprehensive processing, and review of recent relevant literature to explore the application methods, pathways, and effects of BPNN in distillation systems [21].
In the above content, there are many research results related to CIPPs and BPNN in the current research. BPNN has good application effects in the intelligent evaluation. However, there are almost no relevant research results on the application of BPNN to the performance evaluation of CIPPs. In addition, the performance of general BPNN also has certain limitations. It needs to be optimized to meet application requirements. In response to the above issues and the shortcomings of low efficiency and accuracy in current methods, an improved BPNN model based on MHHO is proposed to achieve intelligent evaluation of the CIPP hole walls stability, improving the evaluation effect. It is expected to improve the traditional CIPP hole wall stability evaluation method by introducing intelligent algorithms and optimization techniques, providing more accurate and efficient evaluation tools for the engineering and construction industries. This will not only help to improve the quality and safety of pile foundation construction, but also promote the technological progress and innovative development of the engineering construction industry.
Construction of intelligent evaluation model for the stability of CIPP hole walls based on MHHO-BPNN
In the southeast coastal area, due to the unique geographical location, the bearing capacity of most of the local soil is relatively weak, making it difficult to meet the construction needs of modern construction projects. Therefore, strengthening the foundation with CIPP is very important. The stability evaluation of the borehole wall of CIPPs has also received attention. Based on existing relevant literature and the usage of CIPPs in the southeastern coastal areas, a stability evaluation index system for the borehole wall of CIPPs has been constructed. Therefore, an intelligent evaluation model for the stability of CIPP hole walls is constructed based on the BPNN.
Construction of Index System for Evaluating the Stability of Bored Pile Wall
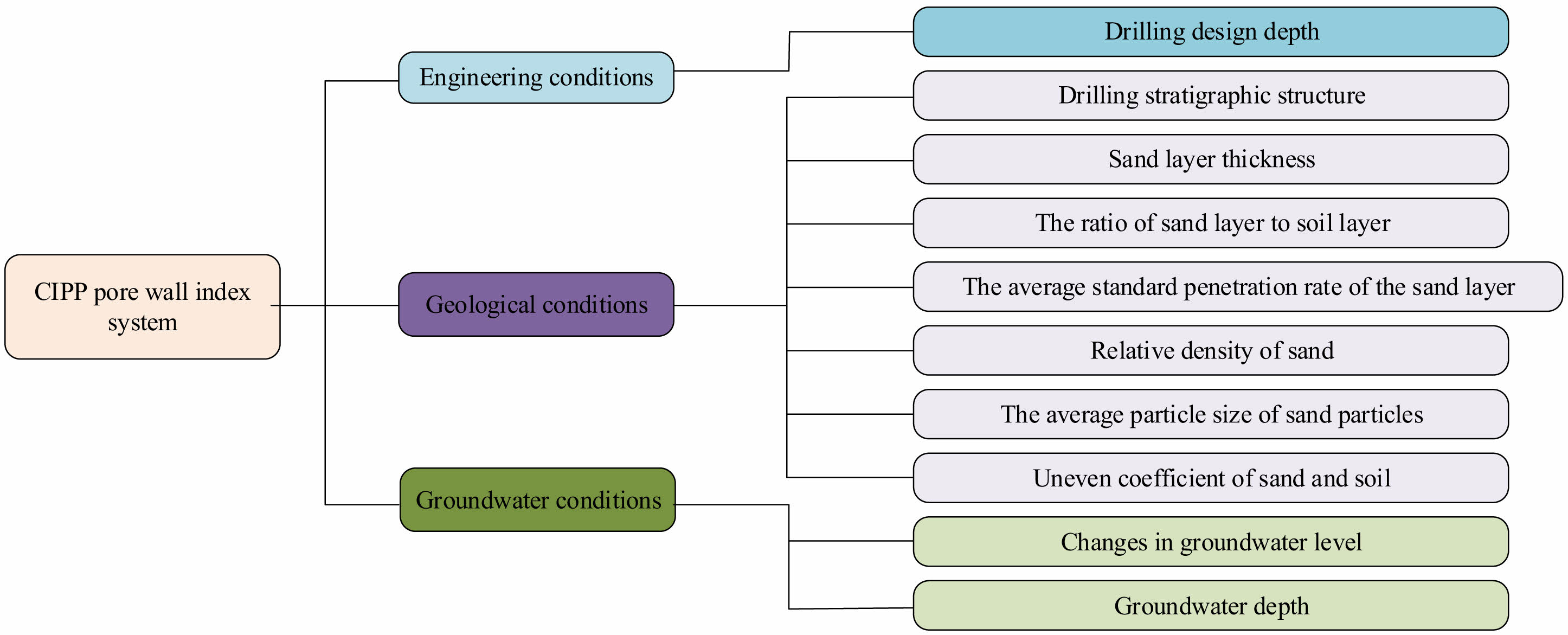
Many factors affect the stability of the borehole wall of bored piles, including geological factors, the quality of the pile itself, and construction methods. To achieve accurate and scientific evaluation of the CIPP hole wall, combined with existing research theories in the southeast coastal areas, the selection of evaluation indicators for the CIPP hole wall is carried out [22]. The evaluation index system for the stability of CIPP hole walls is constructed. Through analysis of engineering data and related research results in the current southeast coastal area, it is found that when the wall of the CIPP collapses, the main collapse area is in the sandy soil layer [23, 24]. Therefore, In the CIPP pore wall stability evaluation index system, sand layer related indicators are more important. Based on the above content, indicators are selected from three dimensions, namely geological conditions, engineering conditions, and groundwater conditions. The evaluation index system of CIPP hole walls is constructed, as illustrated in Fig. 1.
As can be seen from Fig. 1, the CIPP pore wall evaluation index system in this study comprises three main categories: Engineering conditions, Geological conditions, and Groundwater conditions. The selected indicators are designed to reflect the typical geotechnical characteristics of southeastern coastal areas, such as soft ground layers, thick sand strata, and high, fluctuating groundwater levels. For Engineering conditions, Drilling design depth and Drilling stratigraphic structure capture the depth and complexity of borehole disturbance. For Geological conditions, indicators including Sand layer thickness, The ratio of sand layer to soil layer, The average standard penetration rate of the sand layer, Relative density of sand, The average particle size of sand particles, and Uneven coefficient of sand and soil jointly characterize the looseness, uniformity, and stability of subsurface materials. For Groundwater conditions, Changes in groundwater level and Groundwater depth reflect the potential hydrogeological disturbance and pore wall softening effects.
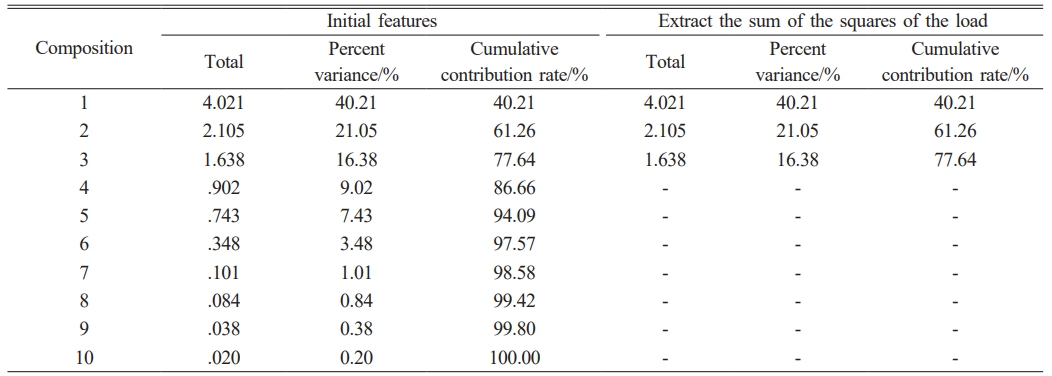
The Analytic Hierarchy Process (AHP) combined with expert scoring method is applied to determine the weights of various indicators in Fig. 1. It is used as the input unit of BPNN for learning and fitting training. From the output results, the stability of the CIPP hole wall is divided into three parts, namely Low risk (Level 1), Medium risk (Level 2), and High risk (Level 3). Depending on the above content, a stability evaluation model for the borehole wall of CIPPs is constructed using BPNN. However, in the current evaluation index system for the stability of CIPP hole walls, there are a large number of indicators that require BPNN to construct more input units. This increases the complexity and affects the efficiency and accuracy. Therefore, Principal Component Analysis (PCA) and Factor Analysis (FA) are applied to reduce the input vector dimension of BPNN and reduce the complexity of the model. Firstly, common factors are extracted based on PCA, as illustrated in Table 1.
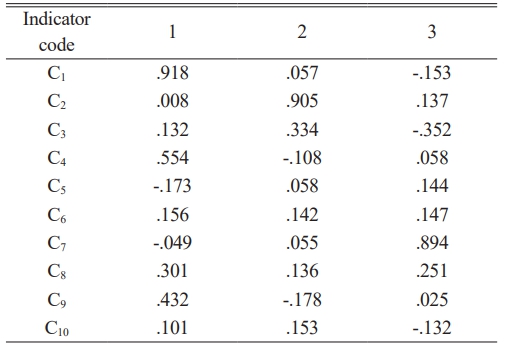
In Table 1, a total of 3 common factors are extracted. Based on these three common factors, the stability of the CIPP hole wall can be roughly reflected. Then, factor analysis is used to extract the indicators with the highest correlation with the three common factors. Thus, the input unit for the CIPP hole wall based on BPNN is obtained. Table 2 displays the results of FA.
In Table 2, the indicators with the highest correlation corresponding to different common factors are obtained. The numerical values and weights corresponding to C1, C2, and C7 serve as input vectors for the BPNN-based stability evaluation model of CIPP hole walls, improving the operational efficiency of the model while ensuring the accuracy. However, the BPNN model has significant shortcomings. The performance heavily depends on the initial parameter selection. If the initial parameters are not selected properly, it will lead to poor evaluation for the CIPP hole wall [25]. Therefore, an enhancement strategy is designed to improve the BPNN to ensure stability evaluation of the CIPP well-bore, providing data support and reference for the reinforcement of the CIPP.

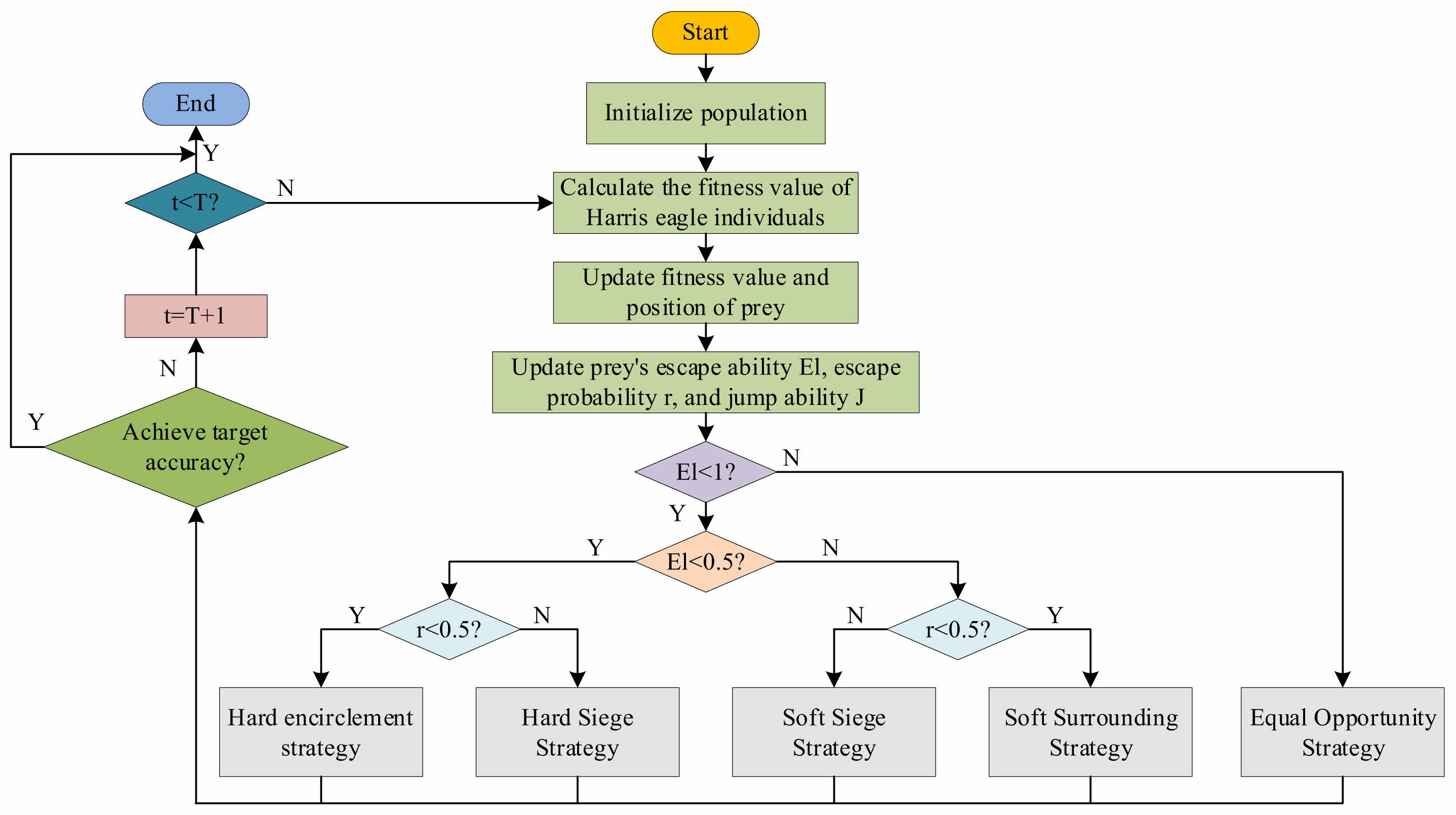
The performance of the BPNN is mainly affected by the initial parameter settings. Therefore, HHO is applied for global optimization to obtain the optimal initial parameters of BPNN [26]. HHO is a nature-inspired metaheuristic algorithm that simulates the cooperative hunting behavior of Harris hawks. In this study, HHO is employed to optimize the initial weights and thresholds of the BPNN, effectively enhancing its convergence speed and prediction accuracy while reducing the risk of falling into local optima. Compared to commonly used algorithms such as GA, Particle Swarm Optimization (PSO), and Whale Optimization Algorithm (WOA), HHO offers advantages including a simpler structure, fewer control parameters, and strong global search capabilities. These characteristics make it particularly suitable for high-dimensional and nonlinear feature input scenarios like CIPP wall stability evaluation. Additionally, a MHHO is integrated to further improve its search diversity and robustness. The basic process of HHO is shown in Fig. 2.
In Fig. 2, the behavior of Harris eagle individuals in the HHO algorithm consists of three stages. It is divided into the search phase, search and development phase, and development phase. During the search phase, the individual Harris eagle is in a state of searching for prey. During the search and development phase, the Harris Hawk has found prey. In the development phase, Harris eagle individuals adopt different strategies to prey on the prey they find based on different situations. The predation strategies of Harris eagles can be divided into soft encirclement strategy, hard encirclement strategy, soft encirclement strategy, and hard encirclement strategy. Among them, in the search phase, HHO simulates Harris Eagles searching for prey based on the opportunity to opportunity strategy. In the search and development phase, HHO adjusts the search and development status of the algorithm by changing the energy factor of prey escape. The HHO algorithm switches between global and local searches. Among them, the escape energy El of prey is the physical strength of simulated prey in reality. The prey’s physical strength is constantly depleted while constantly avoiding the search of the Harris eagle. The value of prey escape energy El continuously decreases. The escape energy El is calculated in formula (1).



In formula (1), E₀ is the initial energy of the prey, with a value of [-1,1]. E is the ability factor, calculated in formula (2).



In formula (2), t, T are the current and maximum iterations of the algorithm, respectively. The predatory strategy of the Harris eagle is determined by the El value and the probability of prey escape r, as shown in Fig. 2. In the soft siege strategy, the update strategy of Harris Eagle is displayed in formula (3).



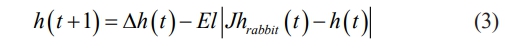
In formula (3), h(t) is the position of the individual in the t-th iteration. Δh(t) is the vector difference between the prey position and h(t) in the t-th iteration. h_rabbit is the prey position vector. J is a random number with a value of [0, 2], representing the jumping energy of the prey. The calculation method is shown in formula (4).



In formula (4), r₅ is a random number with a value of [0, 1]. The update strategy for Harris Eagle in the hard siege strategy is shown in formula (5).



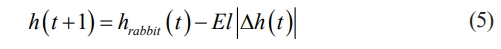
In the soft encirclement strategy, the update strategy of Harris Eagle is shown in formula (6).



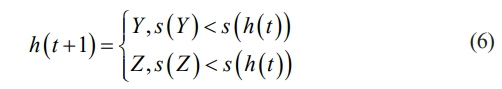
In formula (6), s(•) is the fitness function. Y, Z are calculated according to formulas (7) and (8), respectively.



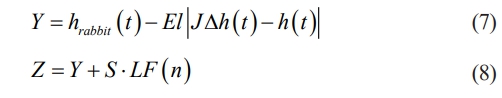
In formula (8), S is a random vector with dimension n. LF( ) is the Levy flight function. In the hard encirclement strategy, the update strategy for Harris Eagle is shown in formula (9).



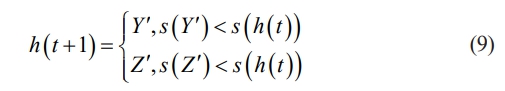
In formula (9), are calculated according to formula (10) and formula (11), respectively.



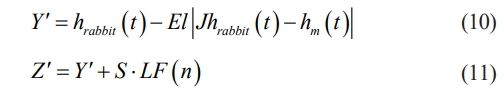
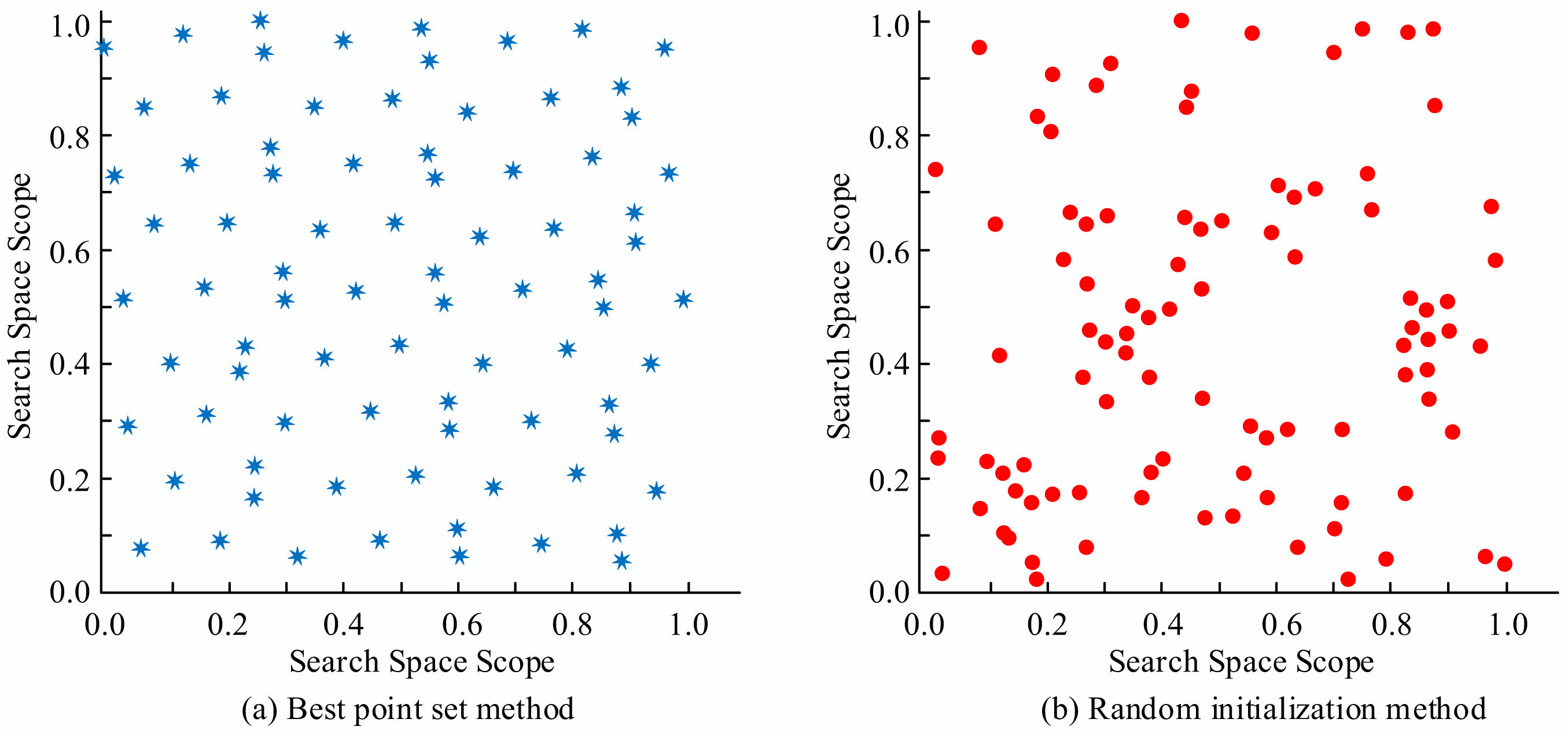
In formula (10), h_m(t) is the average position vector of all Harris eagle individuals in the population. HHO has high search efficiency, simple structure, and excellent performance in high-dimensional problems. However, there are still shortcomings such as being easily trapped in local optima, premature maturation, and overly simple key parameter settings. Therefore, multiple strategies are proposed to improve HHO. Firstly, in commonly used HHOs, the population initialization method is random initialization, which cannot guarantee the diversity of the initial population. Therefore, the algorithm may appear too early, which affects the search efficiency. To address this issue, the best point set method is applied to initialize the population, so that the initial population can be relatively evenly dispersed in the search space. The comparison of two population initialization methods is shown in Fig. 3.
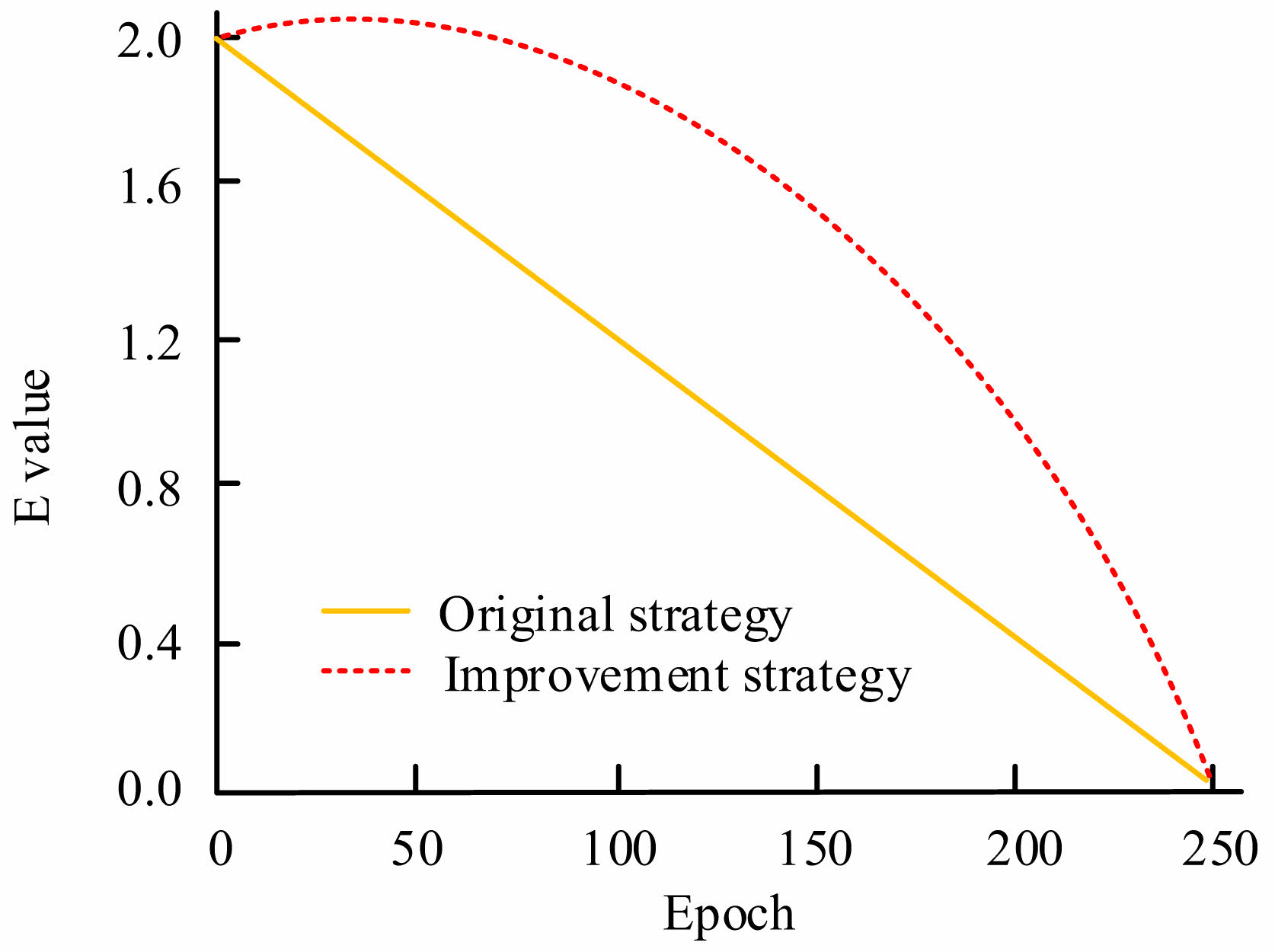
In HHO, the algorithm switches between global and local searches based on the value of El. When | E | < 1 is reached, the algorithm enters the global search phase. Otherwise, the algorithm enters the local search phase. In general HHO algorithms, the E decreases linearly with the increase of algorithm iterations. When the factor is iterated to the later stage, the HHO algorithm is prone to falling into local optimization. To address this issue, an improved E-value update strategy is proposed to achieve nonlinear decrement. Therefore, the HHO algorithm can also perform global search in the later stages of iteration. The improved E-value update strategy is shown in formula (12).



The comparison between the E-value update strategy proposed in the study and the original E-value is shown in Fig. 4.
Based on the above content, the MHHO is utilized to optimize BPNN. To this end, an MHHO-BPNN grouting pile hole wall stability evaluation model is established to improve the evaluation effect and provide data support for the reinforcement of grouting piles. However, its internal decision-making process is often seen as a "black box" and lacks interpretability. This means that users may find it difficult to understand why the model makes specific predictions or classifications. To increase the interpretability of the model, the study adopts Layer wise Relevance Propagation (LRP) technology. Firstly, the MHHO algorithm is applied to optimize the initial parameters and training. Then the LRP technology is applied to analyze the decision-making process of the model. For a given input sample, LRP calculates the correlation score between each input feature and the model output. Allocation rules adopt ε- rules. Ultimately, each feature in the input layer will receive a correlation score. Then, the scores of each layer are normalized. Finally, the correlation score is checked to determine which input features have the greatest impact on the model's prediction results to understand how the model makes decisions based on input data.
Performance analysis of MHHO-BPNN grouting pile hole wall stability evaluation model
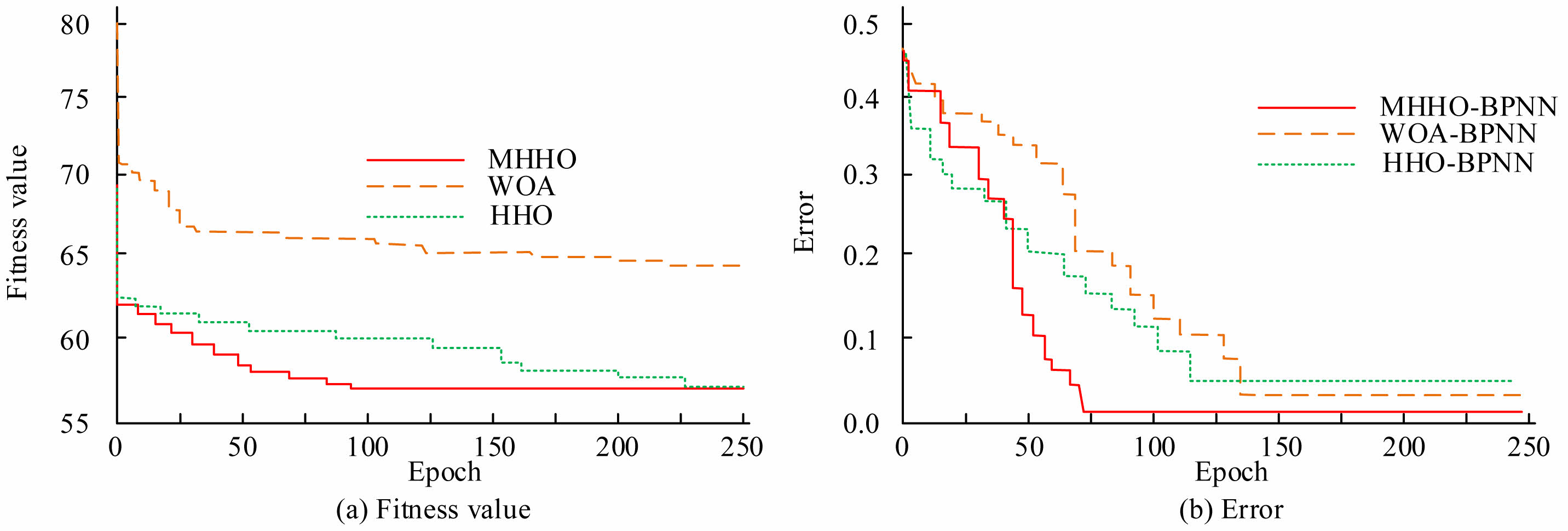
To prove the MHHO-BPNN grouting pile hole wall stability evaluation model, experiments are designed. Firstly, with the consent of the project management personnel for a certain project of CIPP engineering, historical data of the CIPP engineering project is obtained as the original experimental data set. After preprocessing the original data set, according to the 7/3 principle, the experimental data set is divided into training and testing sets. The number of MHHO iterations is set to 100, the population size is 50, the search space dimension is 4, and the learning factor is set to 0.01. The number of HHO iterations is set to 120, and the learning factor is 0.005. The WOA population size is 70. Firstly, the MHHO, HHO, and Whale Optimization Algorithm (WOA) [27] are used to optimize the BPNN to verify the optimization performance of the MHHO, as shown in Fig. 5. The convergence of MHHO algorithm, HHO algorithm, and WOA is shown in Fig. 5(a). The MHHO iterated 100 times to reach the optimal result, which was 58. HHO had more iterations, which may be due to the HHO falling into local optimization in the later stages. Fig. 5(b) displays the training errors of the BPNN model during the training after optimizing the three algorithms. The convergence speed and accuracy of MHHO-BPNN were optimal. The above results indicated that the MHHO had the best optimization effect. The results in Fig. 5 show that the MHHO algorithm can quickly find the optimal parameter combination within a limited iteration, significantly improve the model training efficiency, and is suitable for the requirements of real-time computing and rapid response at the construction site. Meanwhile, the lower training error means that the model has a stronger generalization ability, providing reliable technical support for the rapid stability assessment under different pile foundation conditions in engineering.
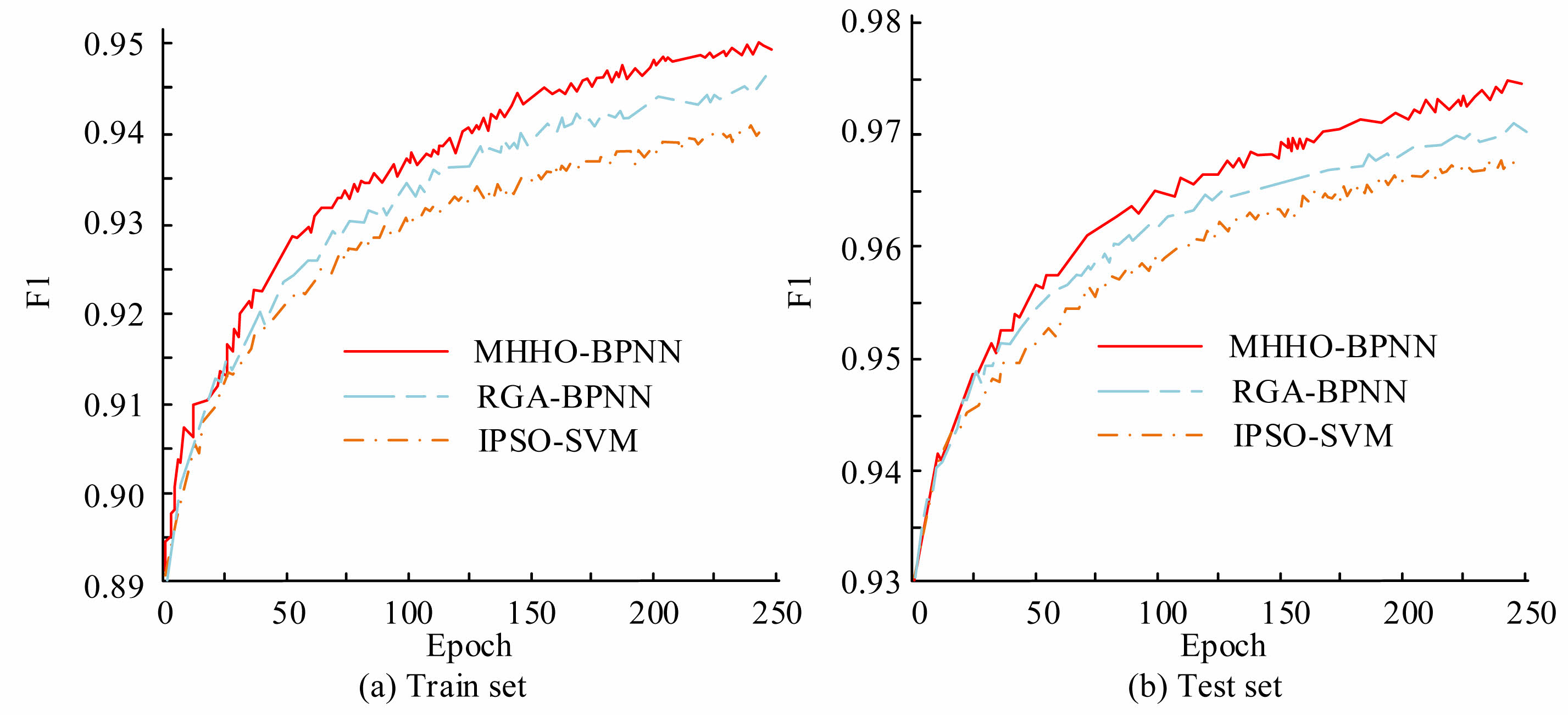
In the field of intelligent evaluation, common models include the BPNN model optimized by random genetic algorithm (RGA-BPNN) and the support vector machine model optimized by optimized PSO (IPSO-SVM). The MHHO-BPNN model is compared with the above two models. Fig. 6 shows the F1 values on the training and testing sets. In Fig. 6(a), on the training set, the F1 of MHHO-BPNN was 0.948, which was 0.045 and 0.097 more than the RGA-BPNN and IPSO-SVM. In Fig. 6(b), on the testing set, the F1 of the MHHO-BPNN was 0.975, which was 0.031 and 0.044 more than the RGA-BPNN and IPSO-SVM. The F1 value reflects the overall balancing ability of the model when accurately identifying high-risk and low-risk samples. The higher the value, the fewer cases of "misjudgment" and "missed judgment" in the model. The improvement of MHHO-BPNN in this index means that it is more reliable in the key task of judging whether the pile hole is stable. It can reduce the risk of missed alarms for unstable pile holes and also lower the false alarm rate for stable pile holes, thereby achieving a more reasonable allocation of reinforcement resources and construction arrangement, and improving the safety and economy of construction.
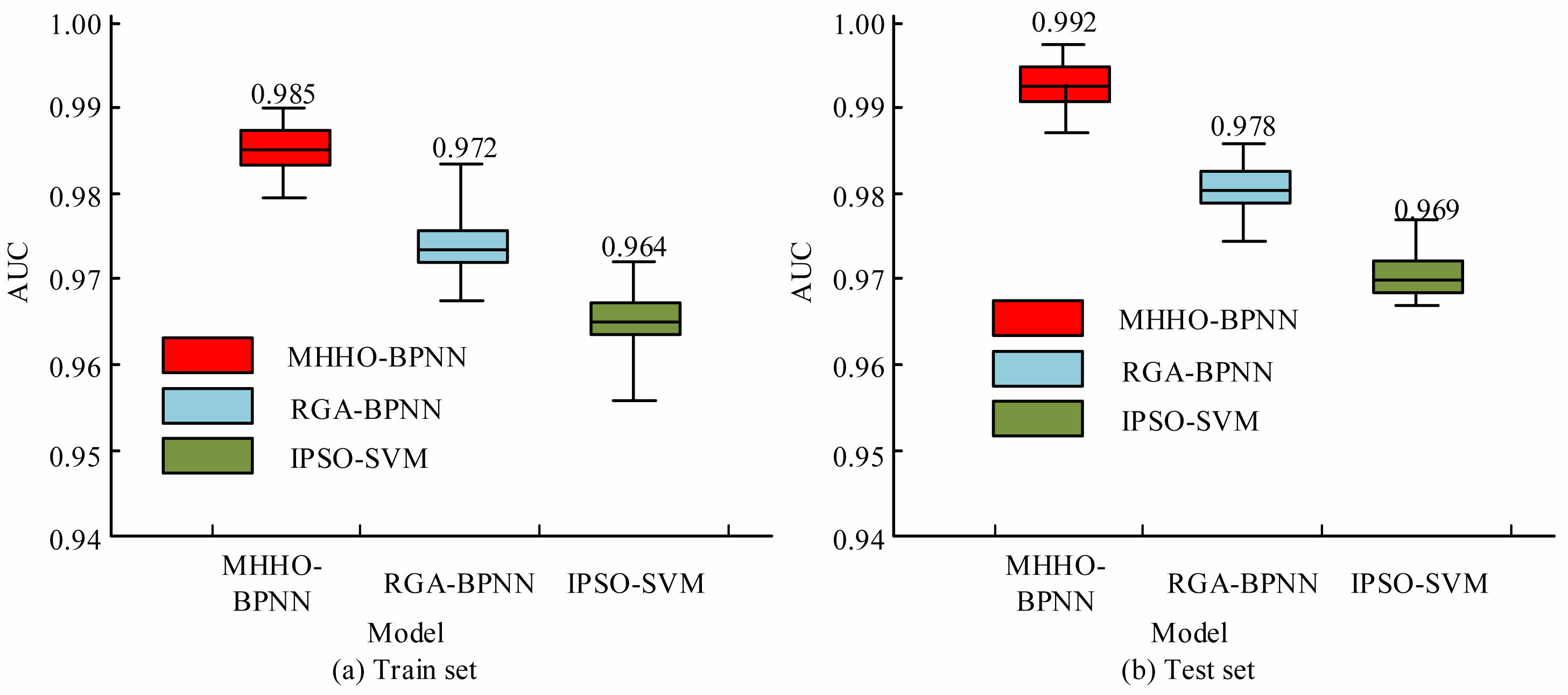
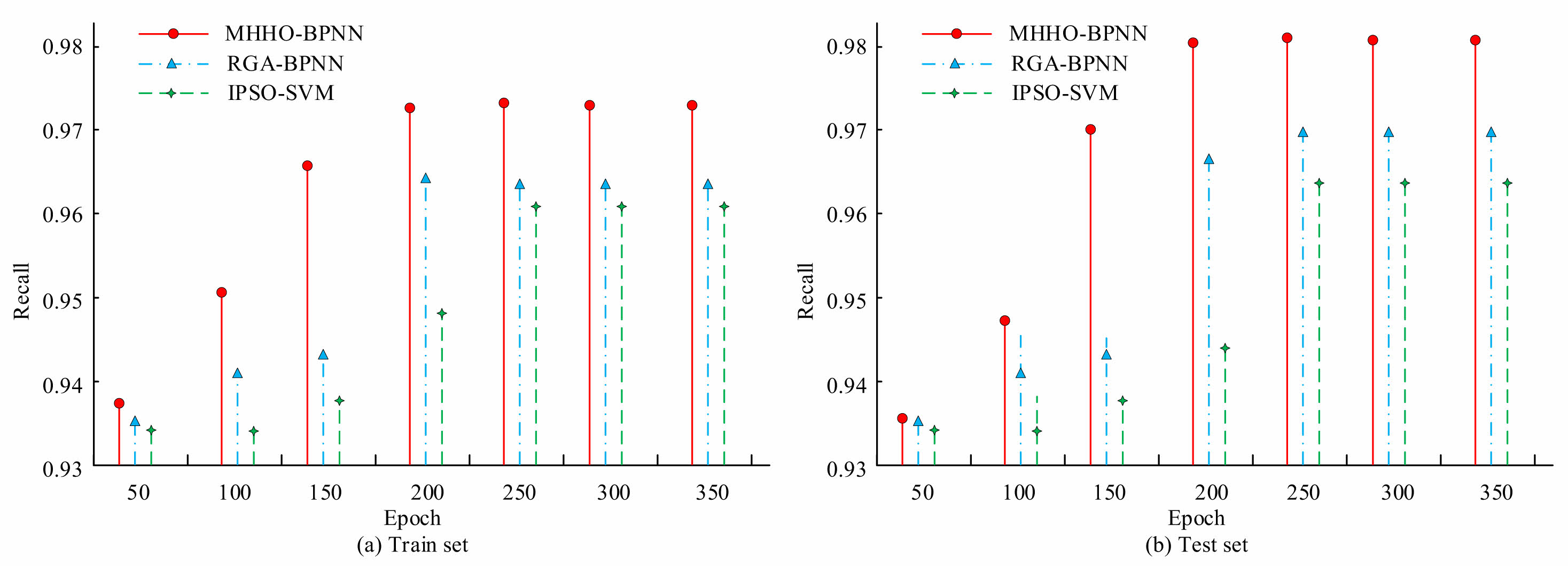
Fig. 7 shows the Recall values of multiple models. The validation adopts k-fold cross validation, where the value of k is selected based on the size and characteristics of the data. The research setting is 50. For each iteration, a different fold is selected as the testing set, and the remaining folds are used to train the model. Through this approach, k different model performance estimates are obtained, specifically in the comparative experiments of MHHO-BPNN, RGA-BPNN, and IPSO-SVM models. The study calculates the Recall of each model in each cross validation iteration. In Fig. 7(a), the average Recall rate of MHHO-BPNN was 0.973, higher than the RGA-BPNN and IPSO-SVM. Similarly, in Fig. 7(b), the average Recall rate of MHHO-BPNN reached 0.984, which was still better than the other two models. Recall rate is a measure of the model's ability to identify "high-risk" samples. The improvement of this indicator indicates that MHHO-BPNN can capture potential unstable pile holes more comprehensively and minimize missed judgments to the greatest extent. This is of vital importance for safety management in engineering practice. It enables the early identification of potential collapse risk holes, allowing for early reinforcement or modification of construction plans. This effectively reduces the probability of sudden accidents and ensures the continuity of the construction process as well as the safety of on-site workers.
Figure 8 shows the Recall values. In Fig. 8(a), the Recall of MHHO-BPNN was 0.973, which was 0.009 and 0.014 more than the RGA-BPNN and IPSO-SVM. In Fig. 8(b), the MHHO-BPNN reached 0.984, which was 0.014 and 0.022 more than the RGA-BPNN and IPSO-SVM. Although the increase in the recall rate is not significant, in the context where the proportion of "high-risk hole positions" at the engineering site is usually low, even a 0.01-level increase in the recall rate means that more potential dangerous pile holes have been identified and reinforced in a timely manner. The enhancement of this capability is particularly crucial in intensive operations and high-risk strata such as sandy soft soil in the southeast coastal areas. It not only reduces the risk of missed judgments but also improves the stability control rate of the entire construction project, offering significant dual values of safety and cost control.
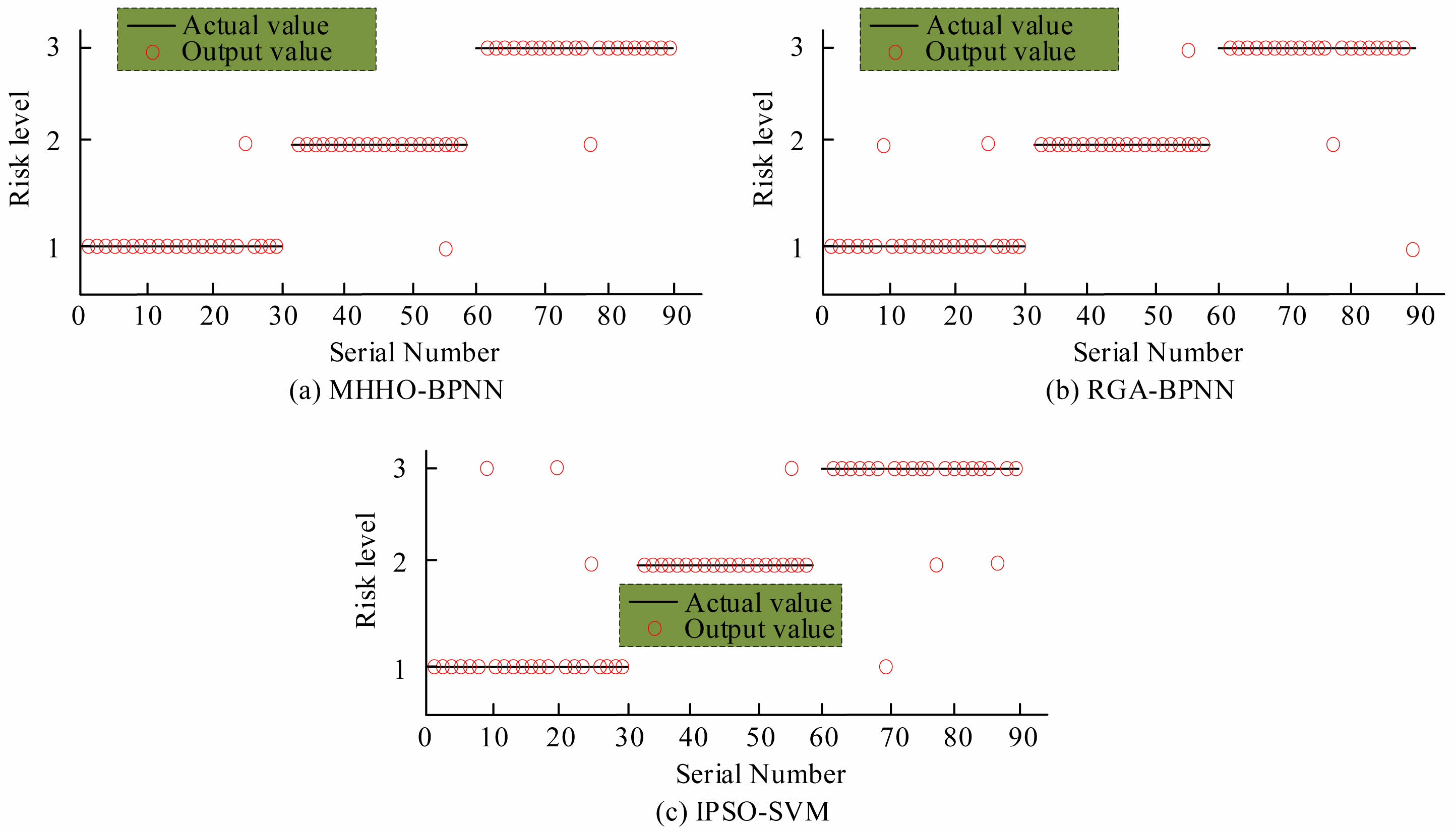
The actual application effects of the above models are analyzed using the experimental data set. The historical data of 90 CIPP construction projects are selected. Among them, there are 30 with an actual risk level of 1, 30 with an actual risk level of 2, and 30 with an actual risk level of 3. Historical data is input into the aforementioned models. The difference in output risk assessment and the actual risk assessment is compared. Fig. 9 is the evaluation accuracy of the three models. In Fig. 9, the accuracy of MHHO-BPNN reached 0.967. The RGA-BPNN was 0.944. The IPSO-SVM was 0.922. The accuracy of the MHHO-BPNN was 0.023 and 0.045 more than that of the RGA-BPNN and IPSO-SVM. The relatively high overall assessment accuracy indicates that the MHHO-BPNN model can provide correct risk judgments in the vast majority of actual construction scenarios. This means that engineering managers can, without relying on subjective experience, achieve automatic identification of risk levels and recommendation of reinforcement strategies with the help of models, thereby improving the efficiency and consistency of risk assessment and reducing resource waste or safety hazards caused by human misjudgment.
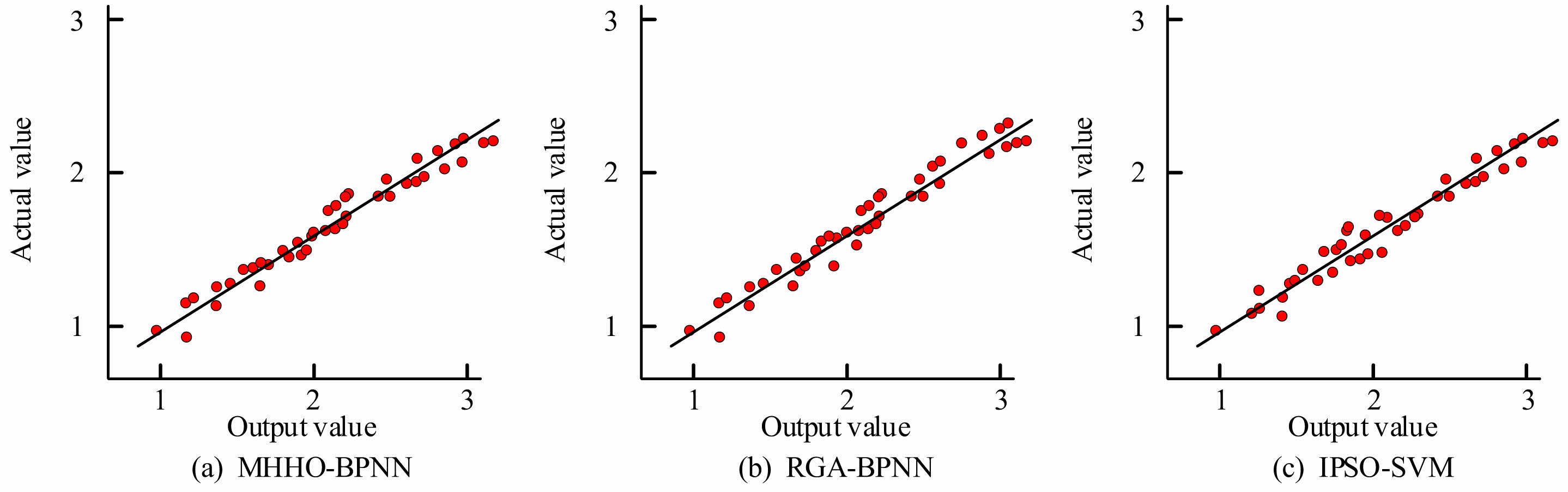
Figure 10 displays the fitting results. In Fig. 10, the fitting degree of the MHHO-BPNN was 0.965. The RGA-BPNN was 0.938. The PSO-SVM was 0.919. The fitting degree of the MHHO-BPNN was 0.027 and 0.046 more than that of the RGA-BPNN and IPSO-SVM. The high degree of fitting indicates that MHHO-BPNN not only performs well on the training samples, but also can reflect the relationship between the complex geological and construction characteristics behind the samples more accurately. This generalization ability enables the model to maintain stable performance when facing new projects, different strata or pile types, and can be reused among multiple CIPP projects. It helps to form a standardized risk assessment process and an automated decision-making mechanism, thereby promoting the transformation of grouting pile construction from "empirical judgment" to "data-driven".

To evaluate the performance of the proposed MHHO-BPNN model for borehole wall stability assessment of cast-in-place piles, two mainstream intelligent evaluation models were selected as benchmarks. The first is RGA-BPNN, which improves prediction performance by optimizing the weights of the BPNN using genetic algorithms and is suitable for nonlinear modeling tasks. The second is IPSO-SVM, which exhibits good classification performance under small-sample and high-dimensional conditions. However, RGA-BPNN is susceptible to the quality of the initial population and suffers from slow convergence, while IPSO-SVM is sensitive to parameter tuning and has limited generalization ability.
In contrast, the proposed MHHO-BPNN model integrates a multi-strategy enhanced Harris Hawk Optimization algorithm to improve the initial weight search of the neural network, thereby enhancing global search efficiency and convergence stability. Experimental results show that MHHO-BPNN outperforms the other models in F1-score, AUC, and recall. Specifically, the F1-scores on the training and test sets reached 0.948 and 0.975, respectively; AUC values reached 0.986 and 0.997; and recall values reached 0.973 and 0.984. In addition, MHHO-BPNN achieved the highest accuracy and fitting degree, at 0.967 and 0.965, respectively. These results fully demonstrate that the MHHO-BPNN model provides high evaluation accuracy and superior performance, enabling reliable intelligent assessment of CIPP borehole wall stability. For instance, under complex geological conditions with rich water in weak sand layers, traditional reliance on empirical judgment may underestimate the risks of unstable hole walls, thereby leading to problems such as hole collapse, deformation of steel cages, or failure of concrete pouring. High-precision models can effectively identify medium and high-risk grade hole positions, enabling construction personnel to take measures such as reinforcement, wall protection delay, and adjustment of drilling rate in advance, thus avoiding accidents from the source.
This provides important data support and reference for the reinforcement and selection of reinforcement methods for CIPP. It has positive significance for improving the safety and quality assurance of construction projects. Future research directions can further explore the optimization potential of MHHO algorithm to improve its performance on more complex problems. In addition, the MHHO-BPNN model can be applied to stability evaluation problems in other fields to verify its widespread applicability. Future work can also focus on integrating this model into actual engineering management systems to achieve real-time and accurate stability evaluation and warning functions, further enhancing the intelligence of engineering management. The practical significance of the research lies in providing an efficient and accurate stability evaluation method for engineering construction, which helps to improve the quality and safety of engineering. Its management significance is reflected in providing scientific and reliable decision support for project management personnel, which helps to achieve refined management of engineering projects and optimize resource allocation.