- Prediction of high-temperature explosion spalling in Ultra-High-Performance concrete based on intervention analysis of hybrid fiber performance
Chenhao Xu* and Chunhong Guo
Department of Intelligent Architecture, Zhejiang College of Security Technology, Wenzhou 325016, China
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The high-temperature explosion and peeling of concrete have brought immeasurable negative impacts to both society and humanity. However, the current research on the high-temperature explosion spalling mechanism of Ultra-High-Performance Concrete (UHPC) is relatively shallow, and traditional prediction methods are difficult to achieve effective prediction of UHPC. Therefore, this study proposes a prediction model for high-temperature explosion spalling of UHPC based on the Artificial Neural Network algorithm (ANN) and conducts Hybrid Fiber (HF) performance intervention experiments. Verification showed that the accuracy of the prediction model was 95.95% based on the concrete mix ratio and 87.49% in compressive strength. The performance intervention test of mixed fibers showed that the explosion probability of single-doped polypropylene fibers increased by 100% compared to mixed fibers. When the compressive strength was between 100 and 120 MPa, steel fiber 60 kg/m3 and PP fiber 2 kg/m3 were added, and the high-temperature blast resistance performance of concrete specimens was the best. The results indicate that the proposed high-temperature guarantee peeling prediction model has ideal predictive performance, both in terms of concrete mix proportion and compressive strength. The hybrid polypropylene fibers and steel fibers have a positive effect on the high-temperature explosion resistance of concrete, and the size of concrete is inversely proportional to the probability of explosion spalling.
Keywords: Ultra-High-Performance Concrete, High-temperature explosion spalling, ANN, Polypropylene fiber and steel fiber, Compressive strength, Prefabricated buildings.
The rapid development of urbanization and the increasing demand for buildings have led to the emergence of prefabricated buildings due to the long cycle, high energy consumption, and low efficiency of traditional buildings. Among them, Ultra-High-Performance Concrete (UHPC) is a commonly used material for prefabricated building anchor construction, prefabricated components, and exterior wall decoration, which has ultra-high mechanical performance and durability, as well as good toughness, bonding performance, and impact resistance [1-3]. However, in recent years, the occurrence of multiple prefabricated building fires has attracted widespread attention and strong concern from people. Although UHPC has higher Compressive Strength (CS), tighter microstructure, and lower water cement ratio, relevant studies have found that the fire resistance performance of UHPC is worse than that of Plain Concrete (PC) after high-temperature fire exposure [4, 5]. The phenomenon of High-Temperature Explosions (HTE) has been shown to reduce the load-bearing capacity of UHPC structures. Additionally, it has been observed that HTE can lead to the spalling of the protective layer and the direct exposure of the reinforcement to fire. This, in turn, can trigger early structural failure and endanger the integrity of the entire building’s structural system. However, the current mechanism of HTE for UHPC is not clear, and traditional concrete HTE simulation methods are inadequate for prediction [6]. Furthermore, the understanding of the HTE spalling mechanism of UHPC remains limited in existing studies, which primarily focus on the effect of a single fiber on the performance of UHPC. Therefore, this study innovatively proposes the use of Artificial Neural Network (ANN) to construct a prediction model for UHPC HTE spalling and designs a detailed prediction model from two aspects: concrete mix ratio and concrete CS. Finally, to further illustrate the HTE mechanism of UHPC and analyze its anti-HTE peeling characteristics, this study conducts mixed fiber performance intervention analysis experiments based on the constructed prediction model. It aims to elucidate the mechanism of concrete HTE, summarize the influencing factors of concrete HTE, and improve the HTE resistance of UHPC.
The overall structure of the study consists of four sections. Section 1 summarizes the industry research achievements and shortcomings of UHPC and ANN algorithms. Section 2 designs a Peeling Prediction Model (PPM) based on the ANN algorithm and conducts mixed fiber performance intervention experiments. Section 3 validates and analyzes the proposed PPM and mixed fiber performance intervention experimental method. Section 4 summarizes the experimental results and indicates future research directions.
In prefabricated buildings, fires, high temperatures, and explosions pose a serious threat to concrete structures. Under high temperatures, the cross-sectional area of UHPC components in prefabricated buildings decreases, while the peeling of the protective layer exposes the steel bars directly to the fire. This leads to premature failure of structural components and endangers the integrity of the entire building’s structural system [7, 8]. Therefore, most scholars have conducted various studies on concrete spalling during HTEs. Regarding the impracticality of numerical models for the predicting explosive spalling of concrete based on physical methods in industrial applications, Liu et al. developed a voting set model that combines techniques such as Support Vector Machine (SVM), decision trees, and random forests. By using the XGBoost model for parameter analysis, it was found that Polypropylene (PP) fibers play a major role in preventing UHPC thermal spalling [9]. Iwama et al. simulated the changes in water content from high-strength concrete solids to condensed liquids and free water in micro-pores to elucidate the mechanism of the existence of needle-shaped pores in high-strength concrete during HTEs. By using embedded humidity sensors for prediction, it was found that concrete pinholes can effectively prevent nearby explosive spalling in high-temperature fires [10]. Wang et al. conducted contact explosion tests with different explosive masses to evaluate the blast resistance performance of ultra early strength cement-based self-compacting high-strength concrete slabs. By continuously increasing the number of explosives used to explode concrete slabs, it was found that the reinforcement ratio had a relatively small impact on their blast resistance performance, while the curing time had a positive impact [11]. To study the dynamic performance of reinforced composite slabs composed of ultra-high ductility concrete and UHPC under explosion, Liao et al. proposed using computer programming software for numerical simulation. By analyzing the parameters of the gauge length, reinforcement ratio, and concrete type based on the corresponding on-site explosion time delay, it was found that the maximum deflection of the reinforced mixed slab is inversely proportional to the gauge length and reinforcement ratio [12].
The application of machine learning technology has been extensively studied in various fields, including agriculture, economics, industry, and medicine. The potential of neural network algorithms, such as ANNs, in the field of construction has also garnered significant attention. To integrate waste management with AI, Mater et al. developed an ANN model to predict the CS of green concrete. By using Python software for model construction and training, it was verified that replacing cement with 10% fly ash can reduce the CS of concrete by 9% [13]. Seitellari and Naser developed an ANN model to predict fire spalling in reinforced concrete columns. It took the CS of concrete, the width of reinforced concrete columns, the applied axial load, and eccentricity as input parameters, thus achieving good prediction results [14]. To predict the concrete CS, Moayedi et al. proposed a water cycle algorithm and equilibrium optimizer based on evaporation for simulation. It utilized a neural network processor for input parameters, resulting in a prediction accuracy of 82.59% [15]. Li et al. developed a hybrid model that integrates a backpropagation neural network and beetle antenna search algorithm to improve the accuracy of rock burst intensity level prediction. By using outlier detection and synthetic minority oversampling techniques for preprocessing, a prediction accuracy of 94.3% was achieved in 173 rock burst datasets [16]. Due to the severe impact of chloride ion penetration on the durability of reinforced concrete building structures, Shin et al. predicted the chloride ion diffusion coefficient of concrete. By constructing a regression model based on convolutional neural networks and simulating chloride ion diffusion, the application value of simulation methods based on neural networks in the field of facility maintenance has been improved [17].
In summary, researchers have conducted various explorations on the prediction of HTEs in concrete and the predictive role of neural networks in concrete, and have achieved good results. This helps to understand the residual mechanical properties of UHPC at high temperatures and the concrete spalling caused by fires. However, there are still many gaps in the mechanism of UHPC spalling during HTEs and the influence of fiber content on the anti-HTE spalling characteristics of UHPC. Therefore, this study constructs a prediction model for UHPC-HTE spalling based on ANN. Due to the influence and induction of various factors on the HTE spalling of concrete, this study innovatively designs a concrete hybrid fiber performance intervention test. The purpose is to improve the HTE resistance of UHPC by analyzing the influence of fiber types on the explosion peeling of UHPC.
To enhance the HTE resistance performance of UHPC in prefabricated buildings, a comprehensive summary of the influencing factors of UHPC-HTE is necessary. In addition, it is essential to understand the anti HTE peeling characteristics of UHPC. To this end, the study first uses the ANN algorithm to construct a prediction model for UHPC-HTE peeling. On this basis, a performance intervention experiment design for UHPC hybrid fibers is carried out using a predictive model.
Design of input and output parameters for PPM based on ANN algorithm
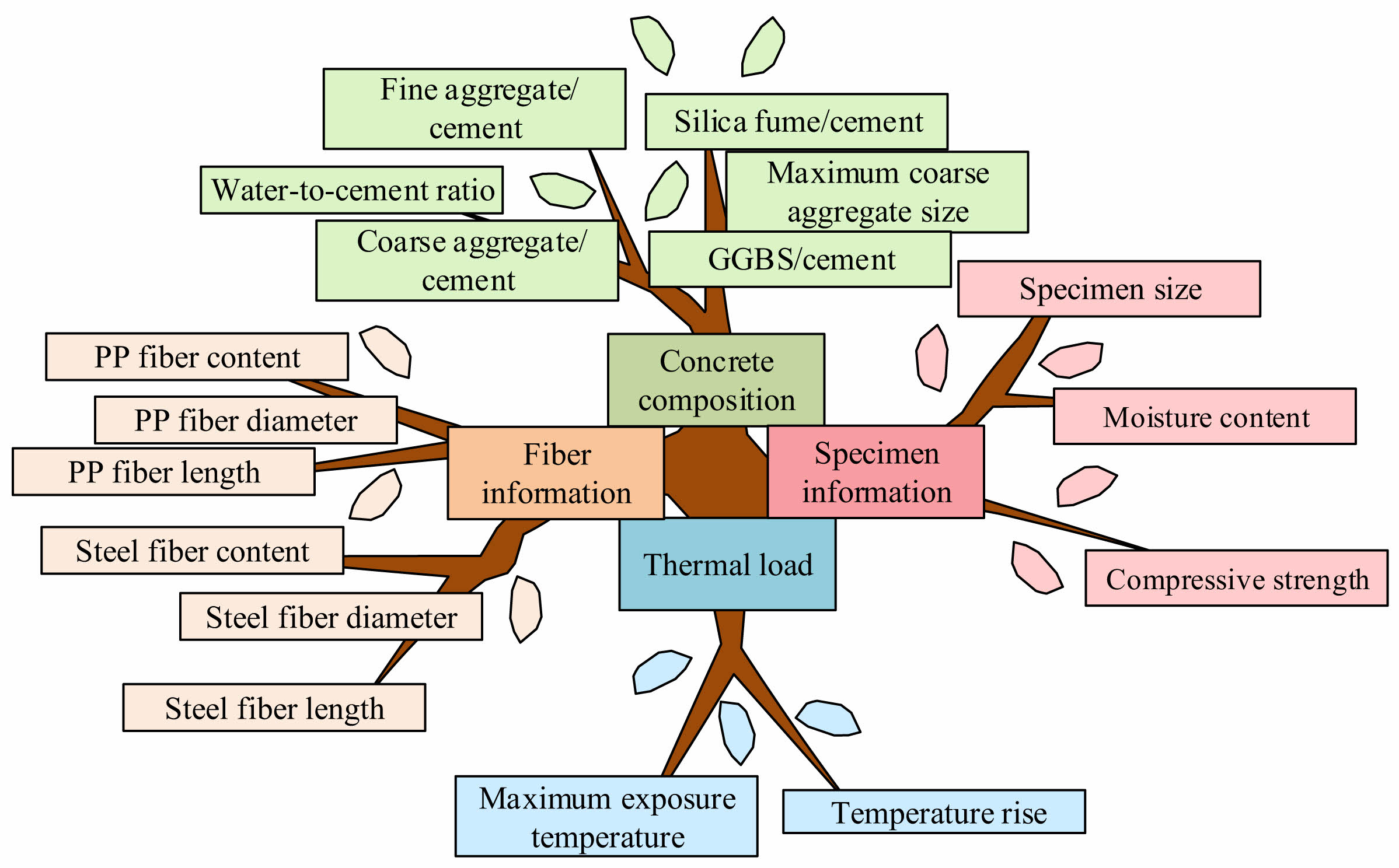
The advancement of computer technology has enabled ANN to be widely applied in multiple research fields. Due to the limited research on UHPC and other concrete HTEs, the influencing factors of UHPC-HTE spalling are first summarized, and then a dataset is established. Meanwhile, this study constructs ANN-1 and ANN-2 models from the perspectives of concrete mix proportion and concrete CS, respectively. Among them, the influencing factors of UHPC-HTE peeling are shown in Fig. 1.
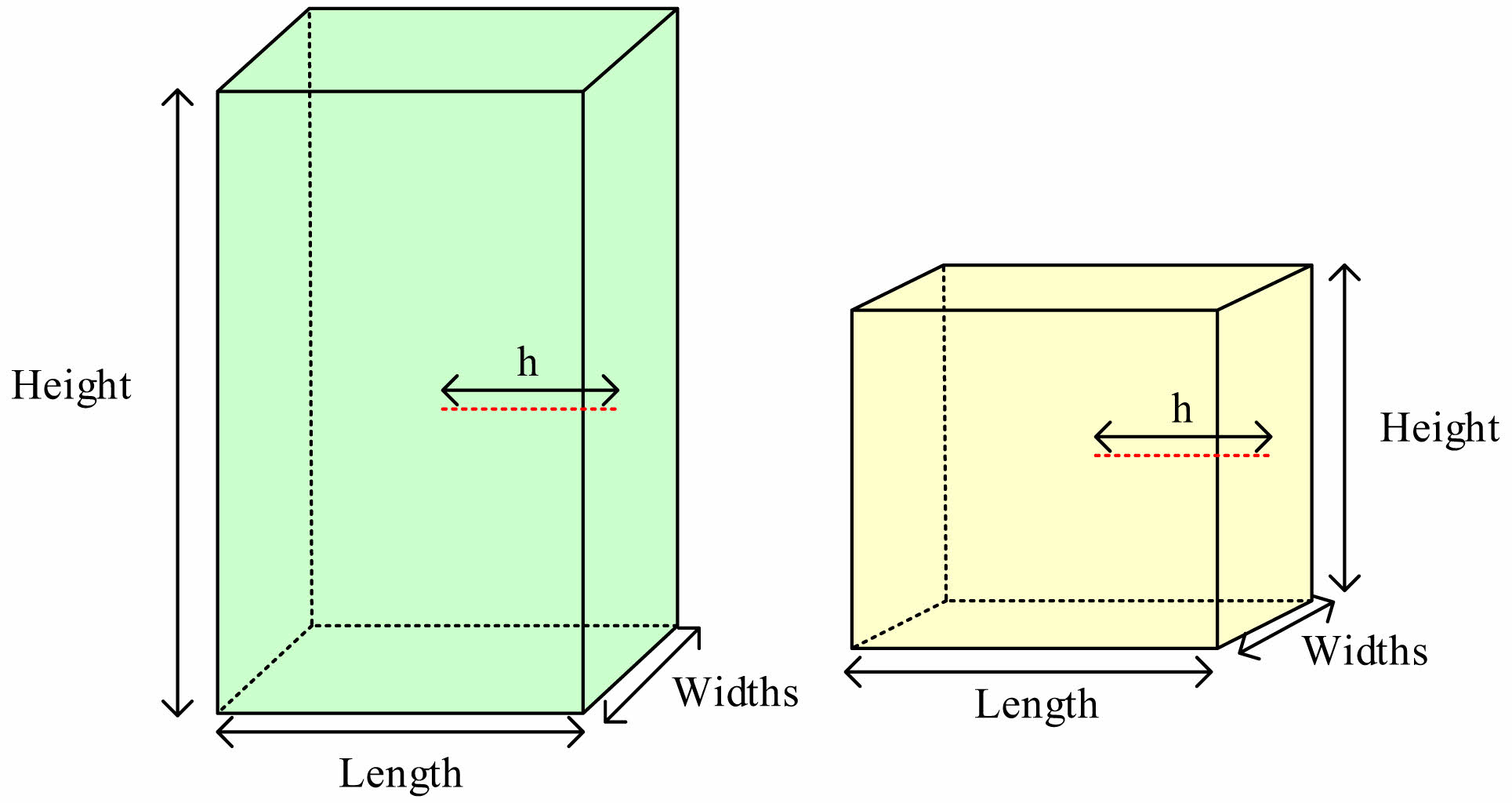
In Fig. 1, the explosive spalling of concrete is a random and complex image that is influenced by multiple factors. Relevant researchers have proposed the theories of thermal wet spalling, thermal stress spalling, and thermochemical spalling to explain the HTE spalling of concrete during HTEs [18, 19]. Therefore, this study mainly considers the influence of thermal wet peeling theory on UHPC-HTE and divides the influencing factors into four categories: concrete composition, thermal load, specimen information, and fiber information. Among them, the concrete composition refers to the number of cementitious materials other than fibers, and the thermal load is the load information of the specimen heated at high temperatures. The specimen information refers to the information obtained through testing after the specimen is formed and cured, while the fiber information represents the information about the fibers added to the concrete [20, 21]. In addition, considering the influence of specimen size, this study sets the specimen size, as shown in Fig. 2.
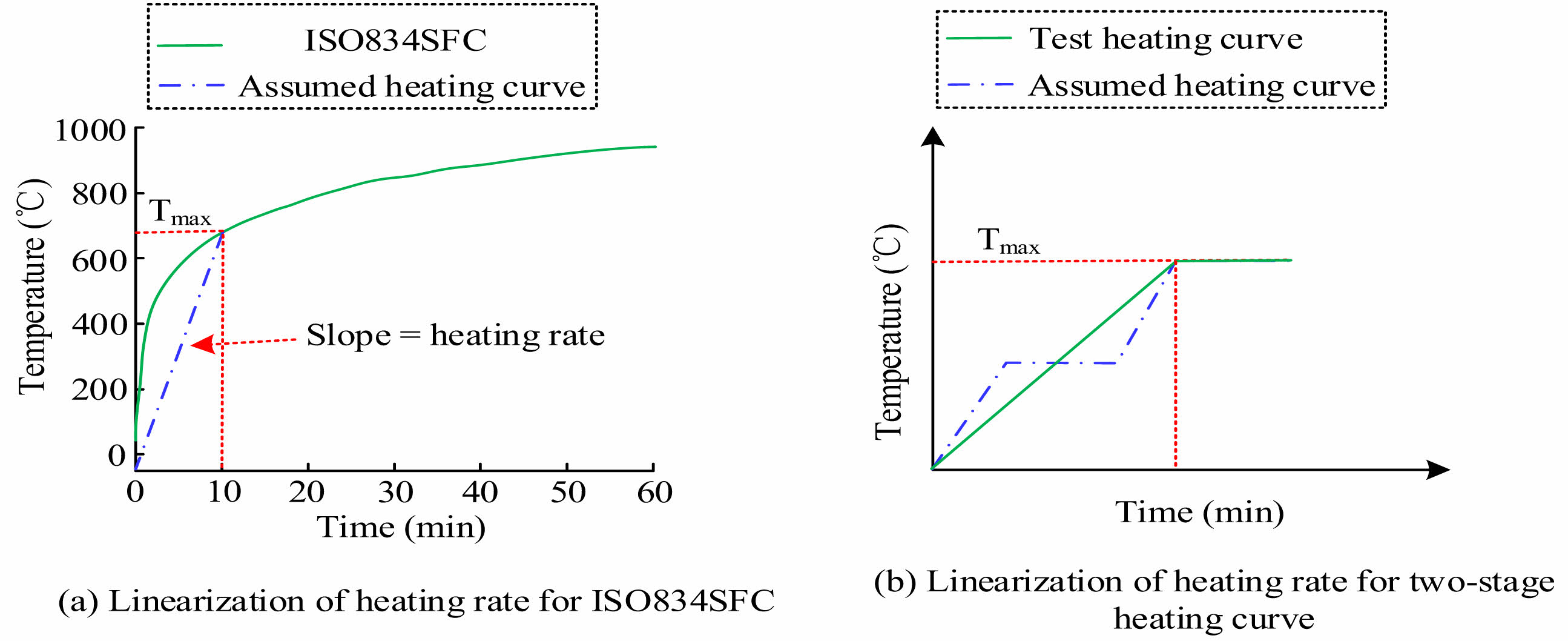
In Fig. 2, h represents the characteristic length of the specimen, which is the shortest accumulation of water vapor from the center of mass to the surface of the specimen. For the length, width, and height of concrete columns, this study assumes that when the height of the specimen is greater than or equal to the length, h is equal to half of the length. When the height is less than the length, h is equal to half the height. Meanwhile, based on the specified input and output parameters of the prediction model, this study establishes a dataset for model training. By referring to previous research results, this study summarizes the processing methods and design ideas of input parameters for relevant experiments [22, 23]. On this basis, the input data of the model have been set with the following relevant rules, as shown in Fig. 3.
Figure 3(a) shows the Linear Heating Rate (LHR) variation curve of the International Organization for Standardization 834 Standard Fire Curve (ISO834SFC). Fig. 3(b) shows the LHR variation curve of the two end heating curves. According to Fig. 3, Rule 1 is set: When the concrete specimen follows the ISO834SFC heating, the heating temperature at 10 minutes is defined as the Maximum Exposure Temperature (MET), and the heating rate is the LHR at 10 minutes. Rule 2: When using a multi-stage heating method, the heating rate is defined as the LHR when heated to the MET. Rule 3: This study defines the Moisture Content (MC) of concrete as 80% of the mass loss rate at 105 ℃ or 120 ℃. Rule 4: The phenomenon of concrete prone to HTE spalling refers to any concrete specimen in a certain mix proportion experiencing HTE spalling.
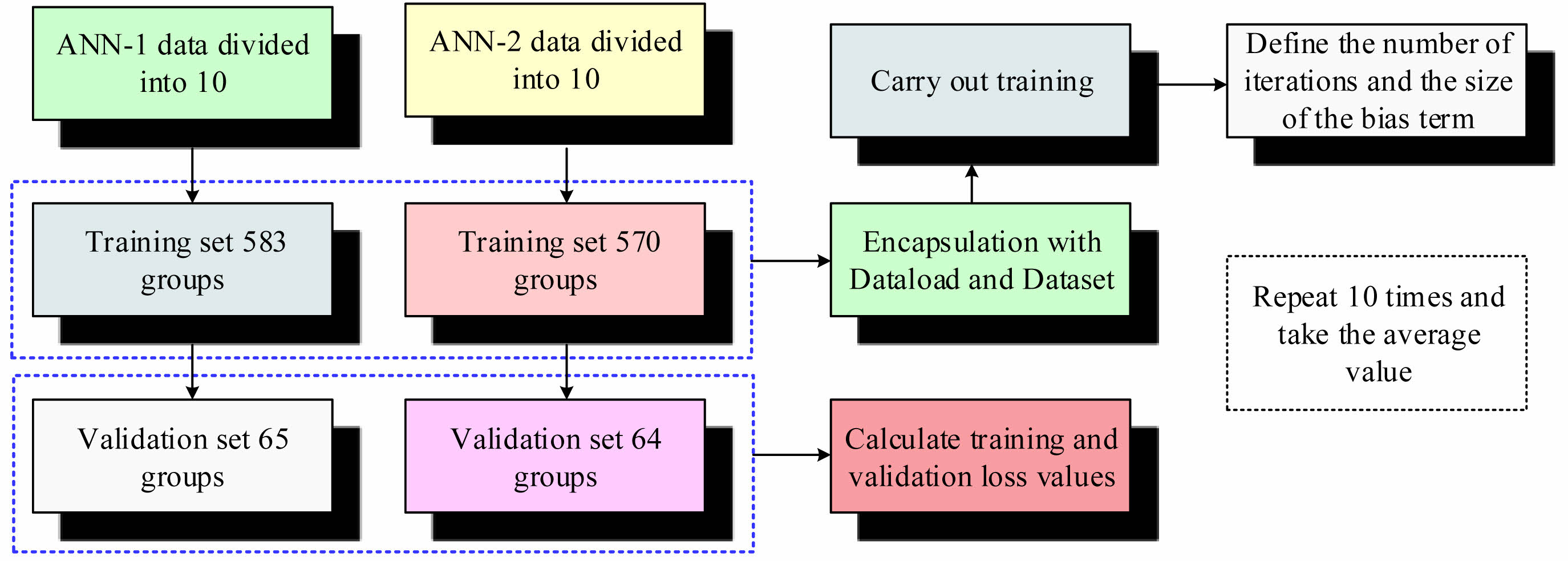
Based on the above rules and relevant UHPC research literature, a total of 648 test data are selected for training ANN-1 and 634 test data are used for training ANN-2 in this study. Meanwhile, this study utilizes K-Fold in Scikit Learn machine learning for dataset partitioning. The division process is shown in Fig. 4.
In Fig. 4, the datasets of the two models are first segmented into 10 subsets. One subset is utilized as validation data for model performance evaluation, and the remaining 9 subsets are taken as training data for model training. Secondly, the 648 sets of data for the ANN-1 model are separated into 583 test sets and 65 validation sets. The 634 sets of data for the ANN-2 model are divided into a test set of 570 sets and a validation set of 64 sets. The model training and validation process is repeated 10 times, ensuring that each subset in the 10 subsets is accurately validated with validation data once. After all learning is completed, the average of the 10 results is tested.
Construction of a PPM based on ANN algorithm
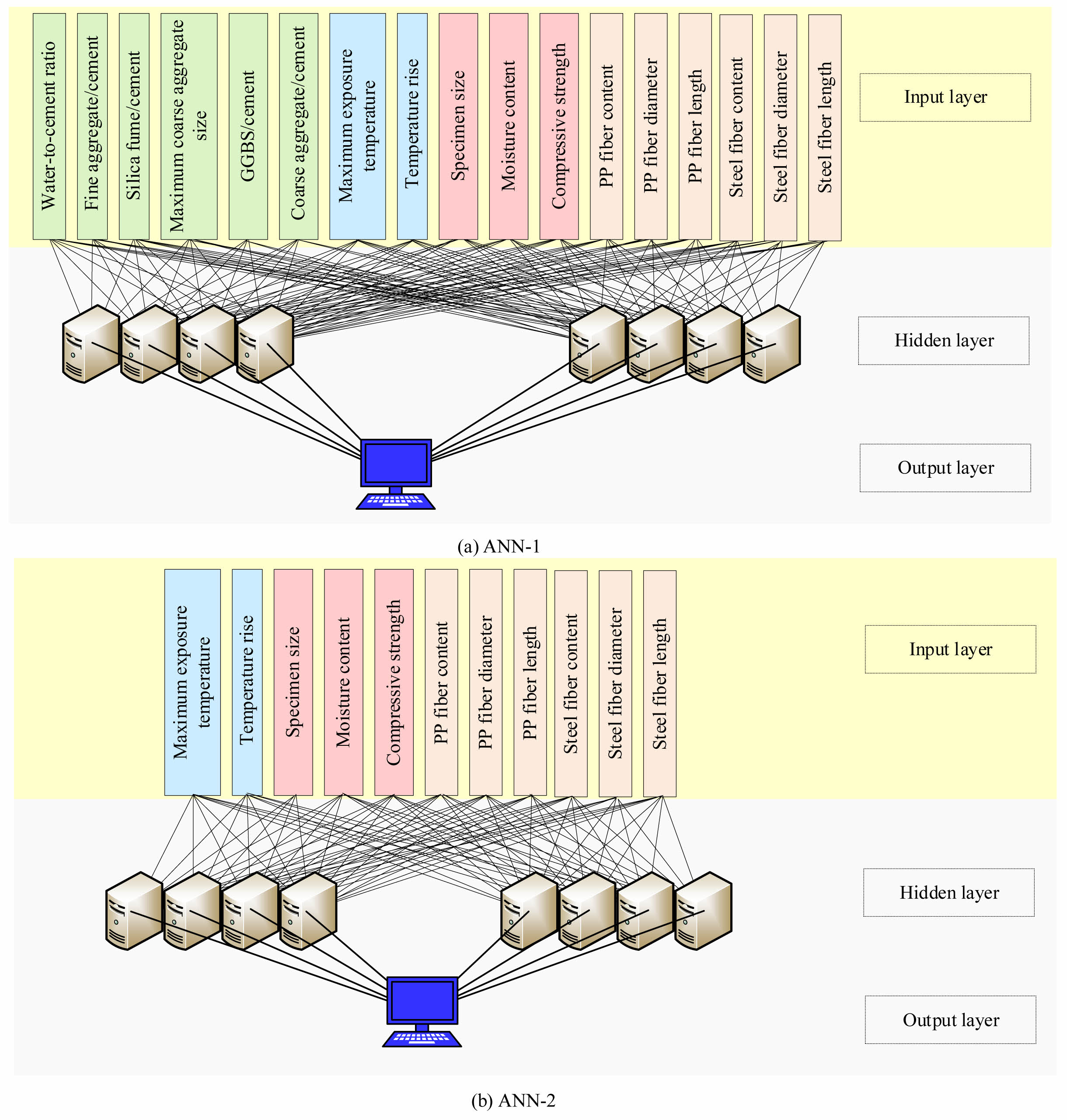
Based on the set input-output parameter rules and model training dataset, this study constructs a UHPC HTE PPM based on the ANN algorithm on the Keras platform. Using packaging classes for model packaging, and using Scikit Learn for model evaluation. The training process of ANN is the learning process. The Input Layer Neurons (ILN) receive input information and transmit it to the hidden meta neurons, which then process the input information from the upper layer and transmit it to the Output Layer Neurons (OLN) [24, 25]. The OLNs perform the final information processing and output the results. This process is called the learning process of ANN, which trains machine learning models. Therefore, this study establishes an ANN-PPM using a sequential model with multiple network layers stacked linearly and optimizes the model using the underlying framework compilation. It mainly includes defining network layers, setting loss functions, optimizers, evaluation criteria, excitation functions, and other parameters. During the process of building the ANN model, it is necessary to define layers and use them to stack a basic network framework [26, 27]. Considering the small amount of research data, low computational complexity, and strong parallelism, this study adopts a three-layer ANN model to predict the HTE peeling performance of UHPC, mainly including the input, hidden, and output layers. Therefore, the input and output of ANN-1 and ANN-2 models are defined as shown in Fig. 5.
Figures 5(a) and 5(b) show the neural network architecture of ANN-1 and ANN-2 models. The neurons of the two models cover the basic conditions and influencing factors for predicting UHPC HTE spalling. The ILNs receive processed 648 and 634 data and transmit them to the hidden layer, acting as signal transmission intermediaries. This study sets the number of hidden layers for both models to be 1, and the initial number of hidden nodes is 20. The output layer is mainly responsible for receiving data from the hidden layer, and processing and outputting the data results by reading the weights and offsets of the hidden layer.
In addition, network parameters also have a significant impact on the model training process [28]. To make ANN fast and effective during the training process, this study limits the relevant parameters. For the batch size and iteration times of the model, this study sets the values of both to be adjusted based on the specific experimental results. ANN commonly uses excitation functions to transform multiple linear input datasets into nonlinear relationships. For the excitation function of the hidden layer, the Relu function is chosen. The Relu function has a fast calculation speed and a more ideal convergence speed [29]. The specific expression formula is shown in equation (1).

In equation (1), represents the Relu function. represents the input value. The output layer only needs to output the target result of "explosive peeling" or "non-explosive peeling". Therefore, this study uses the Sigmoid function as the output function, and the specific formula is shown in equation (2).

In equation (2), represents the sigmoid function. represents logarithm. Sigmoid is commonly used to solve binary classification problems, and its output is event probability. Therefore, the target problem can be set to output a result equal to 1 (explosive peeling) or 0 (non-explosive peeling) [30]. The specific calculation is shown in equation (3).
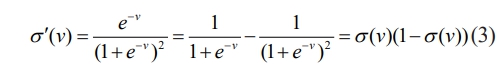
In order for the neural network to output reliable results, it needs to undergo a training process, which is essentially an optimization process that minimizes the error function calculated from the output and target outcomes by identifying a set of weights and biases. Therefore, this study adopts Adam as the optimization algorithm for the ANN. This algorithm has high computational efficiency and is suitable for non-stationary issues with high gradient noise [31]. The Binary Cross Entropy (BCE) between the output and target result is utilized as the error function. Therefore, the probability of the output layer output result being 1 can be obtained from equation (4).

In equation (4), p represents the probability that the output result is 1. u represents the output value. The equation (4) is further merged to yield equation (5).

In equation (5), ω represents the weighting coefficient. From this, the loss function formula for the model output can be further obtained, as shown in equation (6).
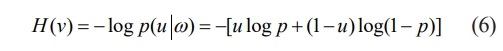
In equation (6), Η(·) represents the loss value. According to the loss formula, for the independent distribution of multiple samples, the maximum likelihood calculation formula can be obtained, as displayed in equation (7).
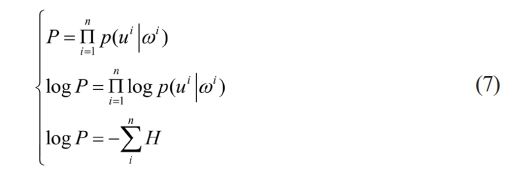
In equation (7), n denotes the number of samples. i is the order of samples P represents maximum likelihood. Therefore, the average error of the sample is calculated as shown in equation (8).
In equation (8), ∂ represents the average error of the sample. The parameter update formula for Adam gradient descent method is shown in equation (9).

In equation (9), βt represents the parameters of the t-th round. γ represents the learning rate. ∂(βt) represents the loss function. ▽∂(βt) represents gradient. When the loss function is minimized, it indicates that the prediction result has the smallest error compared to the actual result, and the model performance is optimal. Therefore, the loss function BCE of the model is combined with the Adam algorithm to obtain the iterative process of the model, and the specific expression is shown in equation (10).
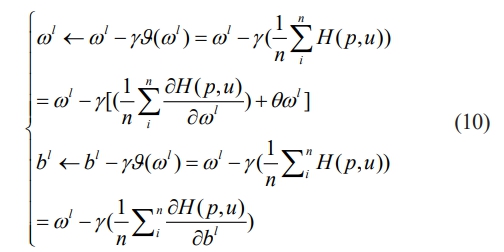
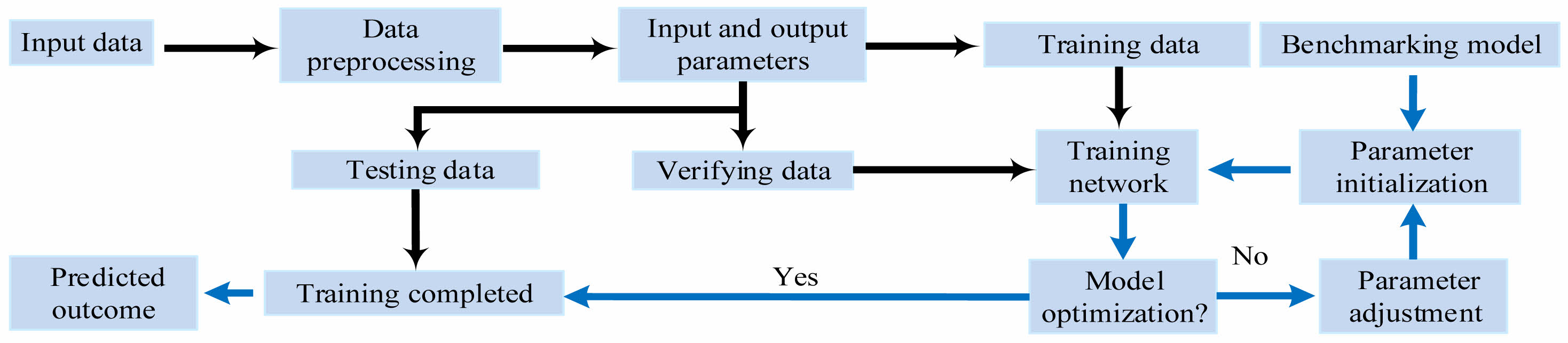
In equation (10), b represents the bias term. l means the number of layers in the ANN network, with a value range of [1, 3]. θ represents the regularization coefficient. Therefore, based on the above parameter settings, the prediction process of the UHPC-HTE-PPM based on the ANN algorithm is shown in Fig. 6.
In Fig. 6, the model first performs data import and preprocessing before making predictions. This study will save the processed data in the form of Comma Separated Values (CSV) and then import the CSV file into the network for preprocessing using the Pandas database. The Pandas database, as a powerful class library in the field of ANN learning, has many data processing methods [32]. Therefore, this study directly utilizes the method provided by Pandas to transform and process the data. Before using the class library for processing, the class library is first imported and random seeds are set. Then, the model is trained and predicted based on input parameters. After data preprocessing and benchmark model construction, the dataset is used for model training. After the training is completed, the program design saves the trained parameters and the best network model locally, so that the saved model state can be directly read during the prediction process. Finally, the network is tested and experimented using UHPC HTE peeling test data.
Experimental design of hybrid fiber performance intervention based on ANN algorithm
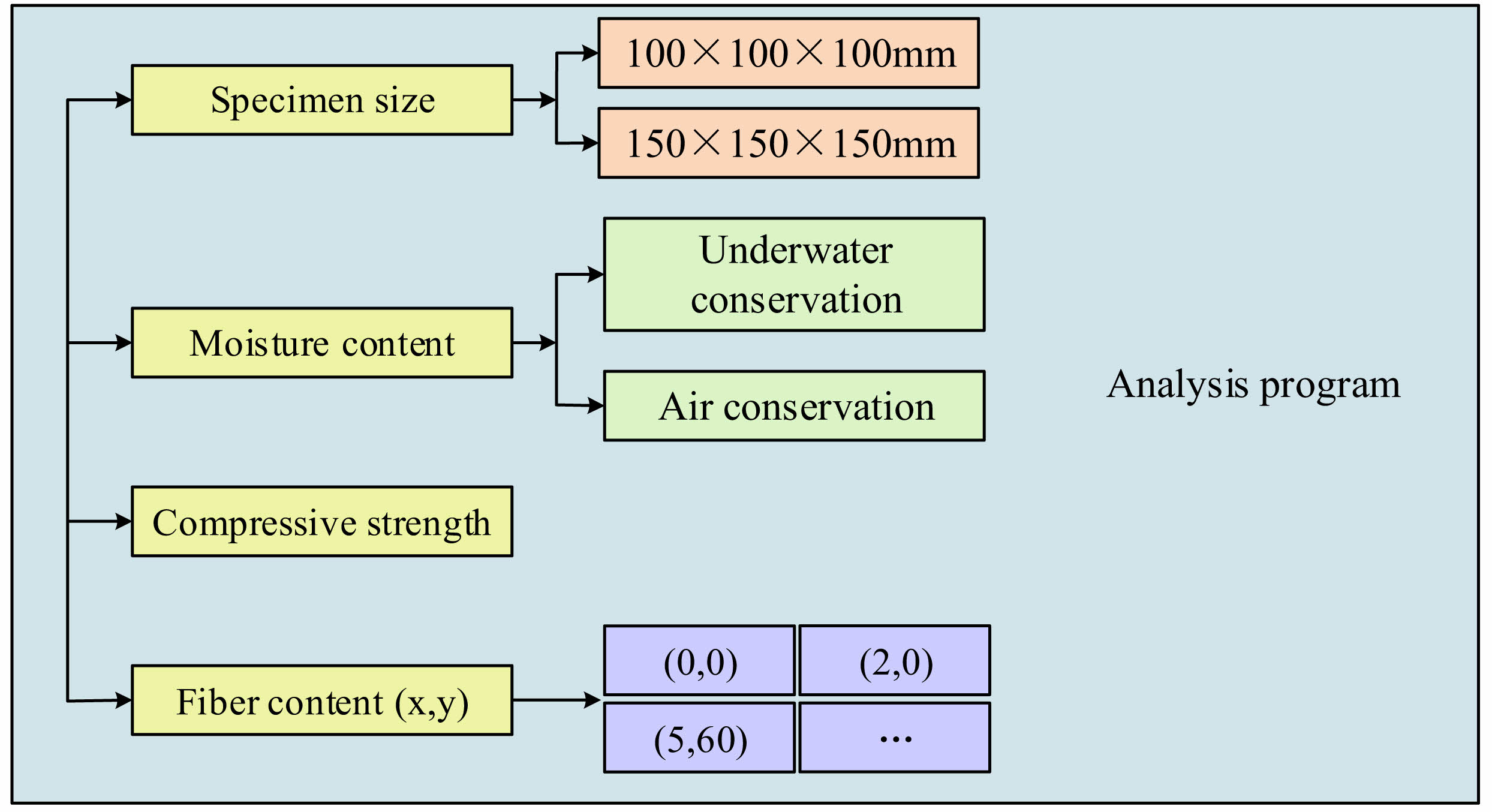
To analyze the influence of the fiber content of UHPC on its resistance to HTE spalling characteristics, based on the proposed ANN algorithm and a spalling prediction model, this study further conducts an experimental design for the intervention analysis of hybrid fiber performance in UHPC thermal explosion spalling. Firstly, PC, PP High Performance Concrete (PPHPC), PPUHPC, and Hybrid Fiber Reinforced UHPC (HUHPC) are used as four research objects. Two different specimen sizes are set up for UHPC HTE peeling tests. The dimensions of the specimens are 100×100×100 mm cubes (specimen A) and 150×150×150 mm cubes (specimen B), respectively. At the same time, the experiment is set to include 24 types of concrete mix proportions, including 7 types of PC, 4 types of PPHPC, 3 types of PPUHPC, and 10 types of HUHPC. Based on the experimental results and predictive model, further intervention experiments are conducted on the performance of hybrid fibers.
The tests are first heated in a standard high temperature furnace equipped with specimen support racks to ensure stable placement of the specimens at high temperatures. In addition, thermocouples and a data acquisition system are installed to monitor the temperature changes on the surface and inside the specimens in real-time, and a high-speed data logger is equipped with a sampling frequency of 100 Hz. The study is conducted using a standard UHPC mix comprising of P-O 52.5 cement (1000 kg/m³), silica fume (100 kg/m³), fine sand (600 kg/m³), medium sand (800 kg/m³), water (200 kg/m³), and high-efficiency water reducing agent (2% of cement dosage). The mixed fibers include PP fibers (with diameter of 20 µm, length of 12 mm, and tensile strength of 800 MPa) and steel fibers (with diameter of 0.2 mm, length of 13 mm, and tensile strength of 600 MPa). The dosage of fibers is designed according to the test and ranged from 0.5-2.0 kg/m³ for PP fibers and from 60-180 kg/m³ for steel fibers. The specific experimental process is shown in Fig. 7.
In Fig. 7, this study mainly selects PP fiber and steel fiber as the main fibers added to concrete, and sets the PP fiber as x and the steel fiber content as y, and represents the two types of fiber content in coordinate form. Based on practical engineering cases and a large amount of experimental data, this study systematically sets up 14 fiber dosage combinations. It mainly includes (0,0), (2,0), (4,0), (6,0), (1,60), (2,60), (3,60), (4,60), (5,60), (6,60), (2,90), (2120), (2150), and (2180), and the dosage unit is kg/m3, which is the mass of fiber added per unit volume of concrete. In addition, CS mainly refers to the four types of concrete obtained through different mix proportions. To make the test specimens more suitable for practical construction projects, this study sets the MC of specimen A to be cured in water and specimen B to be cured in air. Compared with traditional methods, ANN is able to handle complex nonlinear relationships and consider the combined effects of multiple factors, thereby improving the prediction accuracy. This study uses ANN algorithm to construct a high-temperature spalling prediction model for UHPC in terms of concrete mix proportion and CS, and conducts intervention experiments by changing fiber types and additives. The complex nonlinear mapping between input and output data has been established, improving the efficiency of UHPC high-temperature peeling prediction.
|
Fig. 1 UHPC HTE spalling influence factors. |
|
Fig. 2 Schematic diagram of the length of the specimen prism. |
|
Fig. 3 Schematic representation of rules 1 and 2. |
|
Fig. 4 Predictive model training dataset segmentation process. |
|
Fig. 5 Fully connected feedforward neural network architecture for model. |
|
Fig. 6 Flowchart of UHPC-HTE spalling prediction model based on ANN algorithm. |
|
Fig. 7 Intervention test on hybrid fiber performance based on ANN algorithm. |
To reasonably elucidate the mechanism of UHPC-HTE spalling and verify the effectiveness of the spalling prediction model based on the ANN, this study first conducts UHPC-HTE spalling experiments based on the prediction model. The experimental results are used as data to validate the peeling model performance. The prediction model proposed by previous researchers for comparison of prediction accuracy is introduced. Finally, based on the designed mixed fiber performance intervention experiment, a mixed fiber performance intervention analysis is conducted.
Validation analysis of PPM based on ANN algorithm
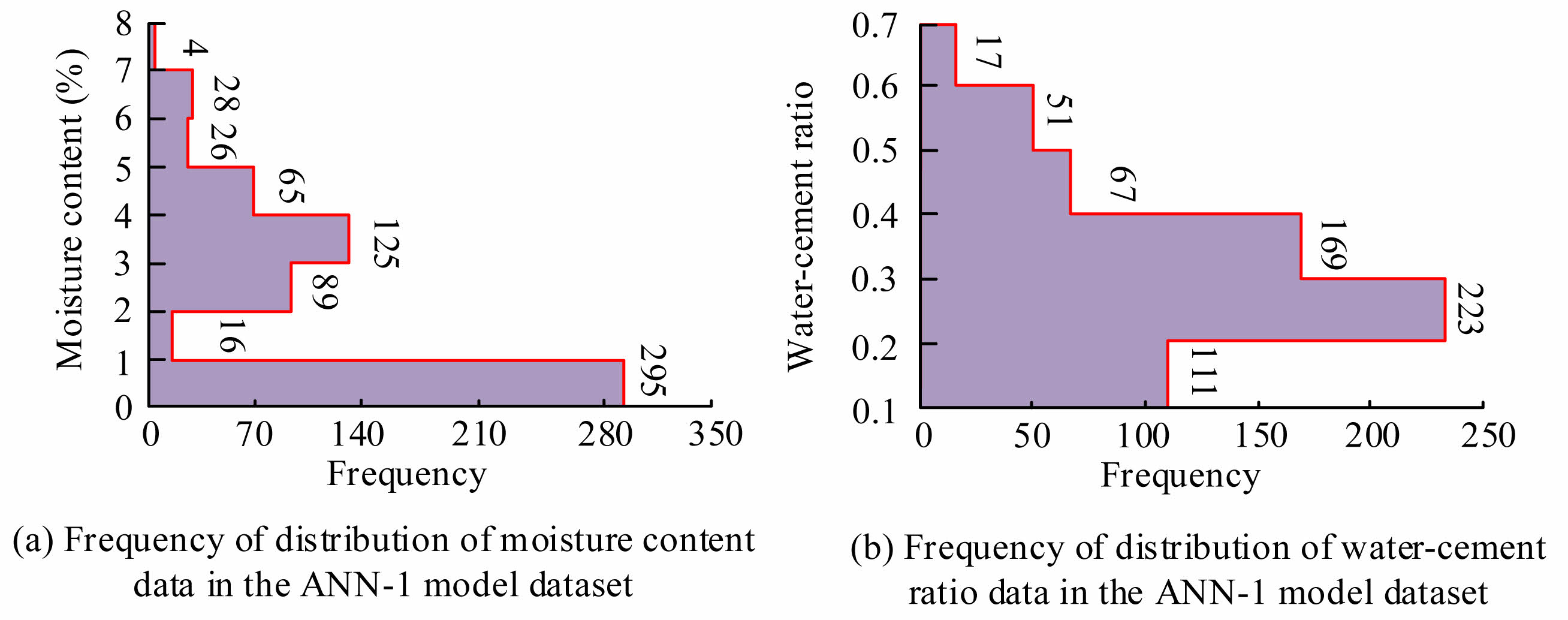
To verify the limitations of the PPM based on the ANN, this study first conducts UHPC-HTE peeling tests and validates the model based on the results. To ensure the rationality and reliability of the experiment, different mix proportions of the PC7 group, PPHPC4 group, PPUHPC3 group, and HUHPC10 group are designed for the HTE peeling test. A total of 4 experiments are conducted, and 96 sets of test results are obtained. On this basis, ANN-1 and ANN-2 models predict concrete HTE spalling based on 96 sets of experimental results. The ANN-1 model is a prediction model for concrete mix proportions. Therefore, this study first analyzes the frequency distribution of MC and water cement ratio in the dataset, as shown in Fig. 8.
Figure 8(a) shows the distribution frequency of MC data obtained by ANN-1 from the dataset. When the MC of concrete is 1%-2% and 7%-8%, the data distribution frequencies in the dataset are 4 and 16, respectively. Compared to Fig. 8(b), the data distribution frequency is highest at a water cement ratio of 0.2-0.3. The frequency distribution of MC and CS of the ANN-2 CS model in the dataset is shown in Fig. 9.
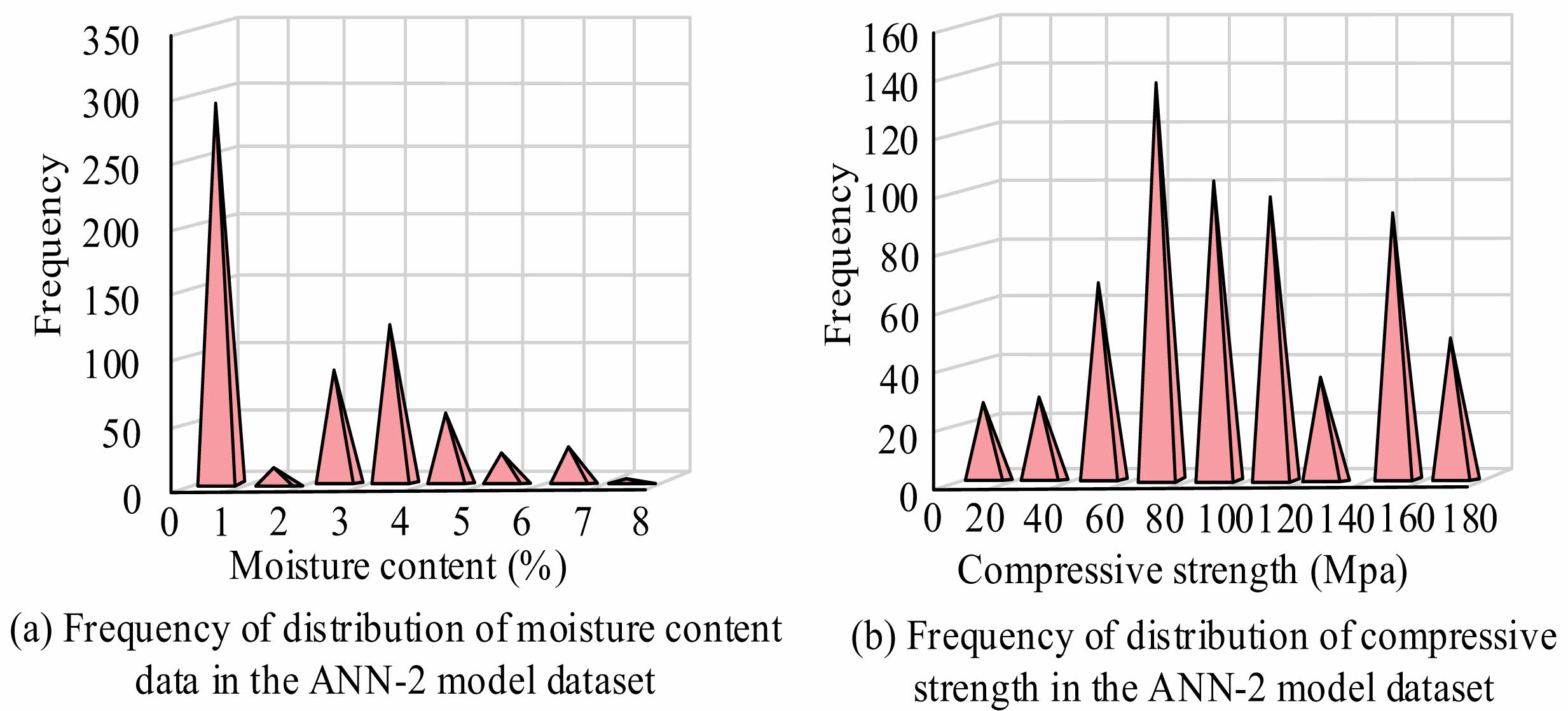
In Fig. 9(a), the data distribution frequency is highest at an MC of 0-1%, with 295 sets of data. Fig. 9(b) shows the frequency distribution of CS, with the data at 60-80 MPa having the highest frequency distribution. The frequency of data distribution is inversely proportional to the increase in MC, while the CS shows a regular change. Based on the data frequency distribution of the two models, this study trains them separately. On this basis, the accuracy of model prediction is verified based on 96 sets of data obtained from the experimental results. The verification results of the two models are shown in Fig. 10.
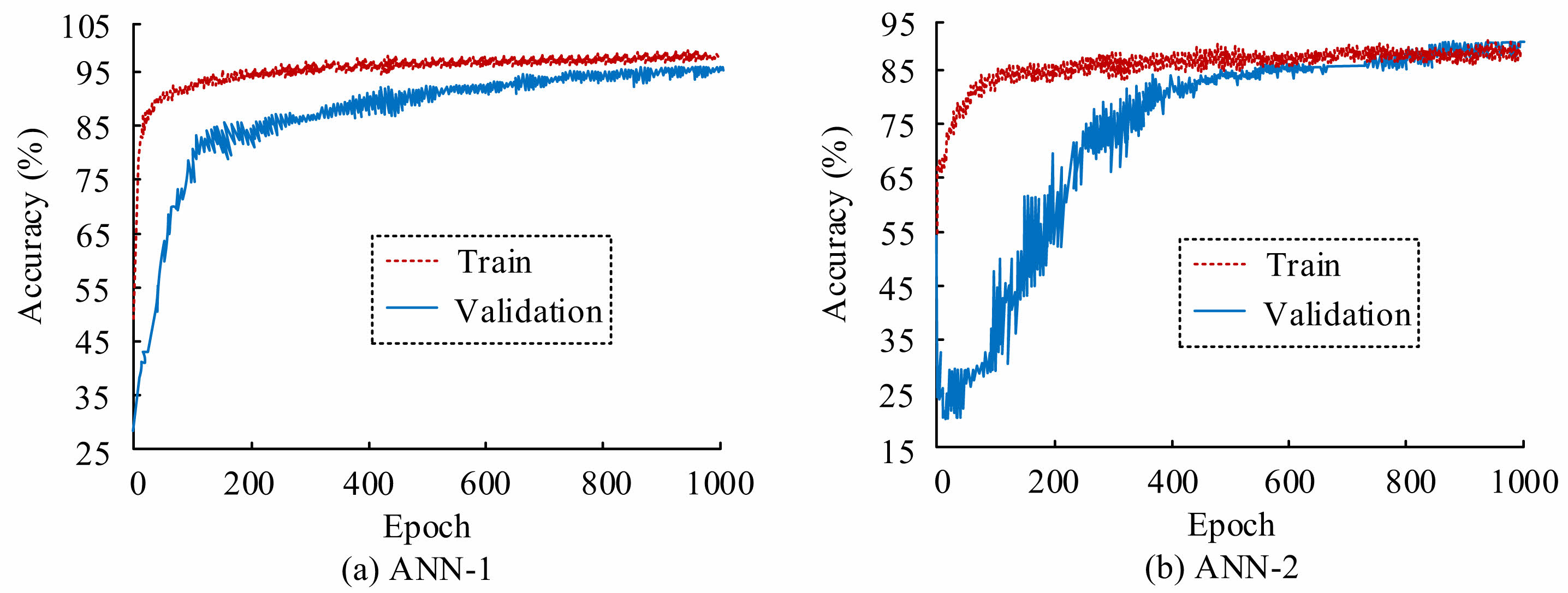
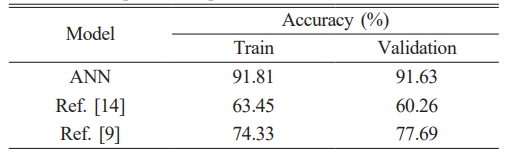
Figure 10 (a) shows the prediction results of the ANN-1. After 1000 iterations, the model is trained with a prediction accuracy of 96.87% and a validation accuracy of 95.03%. In Fig. 10(b), the training accuracy of the ANN-2 model is 86.75%, and the validation accuracy is 88.22%. This indicates that the research model can effectively overcome the negative impact of various data sources, thereby achieving high prediction accuracy. Grounded on the prediction results of the two models, this paper compares their average prediction results with other models. Table 1 shows the results.
In Table 1, the ANN model is more accurate and superior in predicting UHPC HTE spalling. Compared to other methods, the prediction accuracy in the training and validation sets increases by 52.67%, 47.74%, and 30.32%, 22.32%, respectively. Due to the fact that the ANN-1 model is built on the basis of concrete mix proportions, it has more accurate prediction results for UHPC data with different mix proportions. Compared to other models, the accuracy of ANN-2 models based on different CSs is higher. This further confirms the effectiveness and reliability of the UHPC HTE PPM based on the ANN algorithm.
Analysis of performance intervention experiments on hybrid fibers based on ANN algorithm
Based on the 96 sets of experimental data and 4 parameter information obtained earlier, a mixed fiber performance intervention experiment is conducted, resulting in a total of 298 specimen results. Firstly, the effect of various specimen sizes on the resistance of specimens to HTE spalling is verified. The relationship between the CS and MC of two different specimen sizes of concrete cubes and the explosive spalling of concrete is shown in Fig. 11.
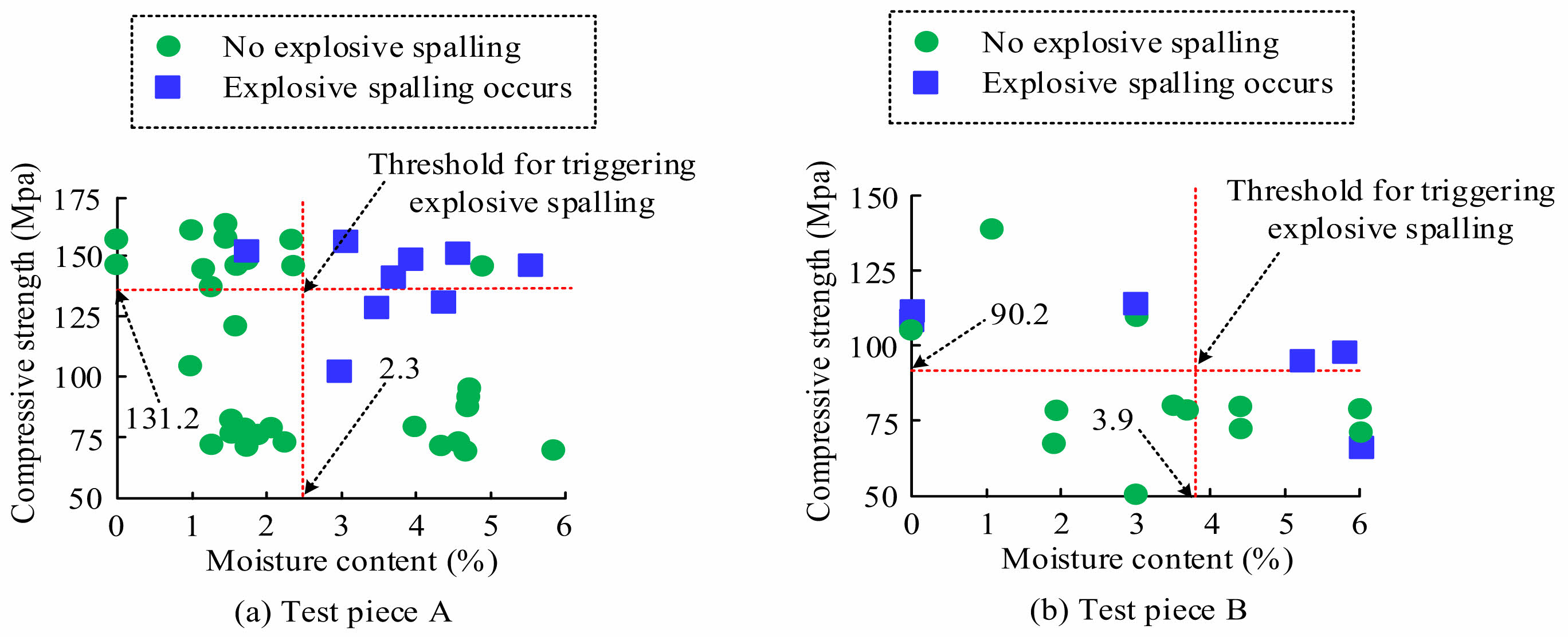
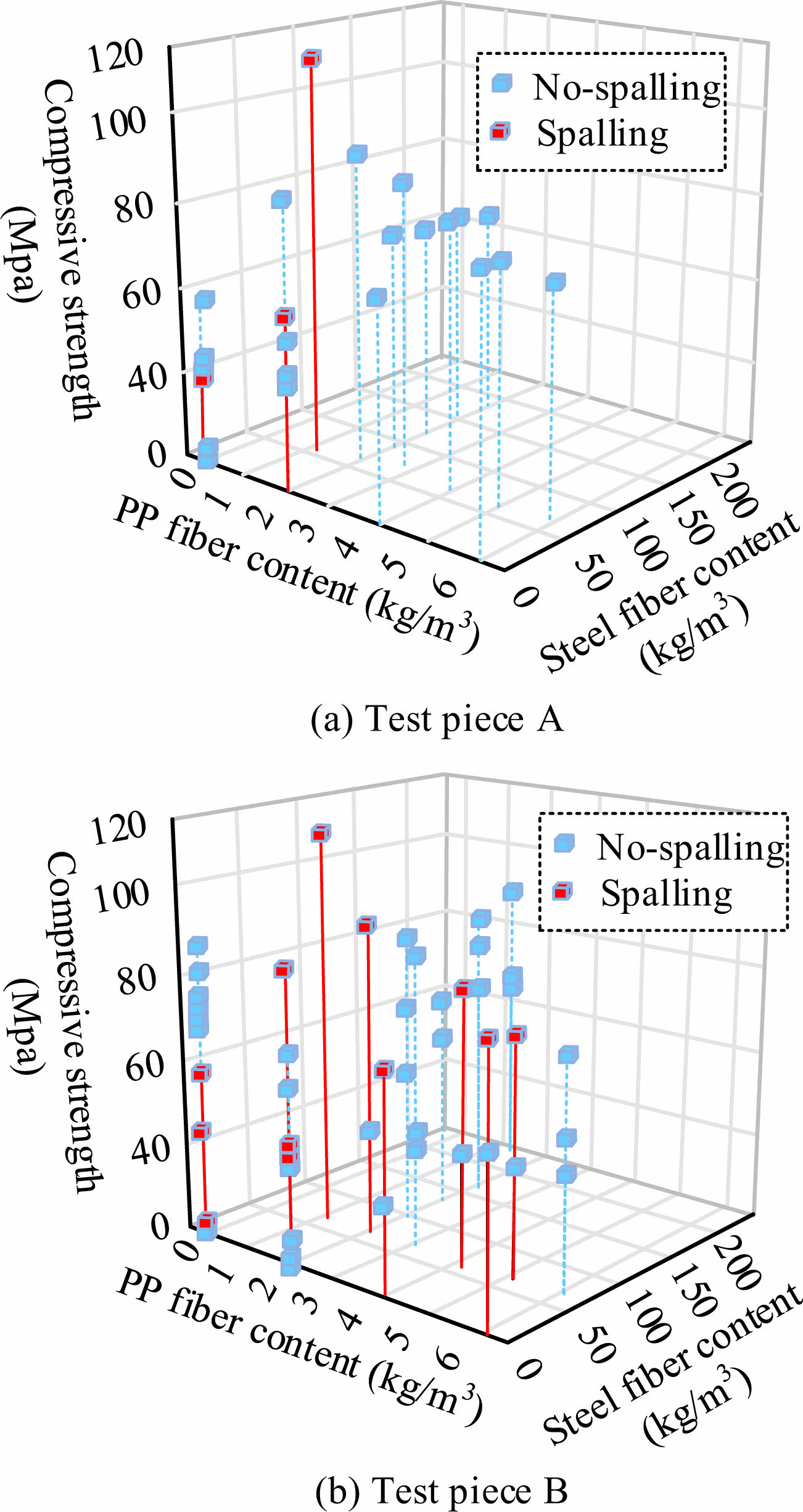
Figure 11 shows the HTE peeling of specimens of two sizes. In Fig. 11(a), the 100×100×100 mm cube (specimen A) is prone to HTE and peeling, with a CS of 131.2 MPa or above and an MC of 2.3% or above. Fig. 11(b) shows the comprehensive effect of CS and MC on the peeling tendency of HUHPC at 150×150×150 mm (specimen B). Specimen B is prone to HTE and peeling when its CS is 90.2 MPa or above and its MC is 3.9% or above. Comparing the peeling conditions of two specimens, the HTE peeling triggering condition of specimen B is significantly lower than that of specimen A. This indicates that the larger the size of the concrete specimen, the greater the probability of HTE peeling.
On this basis, this study conducts different fiber blending settings, as shown in Table 2. There are the dosage distribution of single doped PP fiber (x) and mixed doped PP fiber + steel fiber (x, y), single doped steel fiber (y), and mixed doped steel fiber + PP fiber (x, y). Considering the fiber content in actual engineering and HTE tests, the actual content of concrete fibers set may differ from the distribution of the designed content, but it still has regularity.
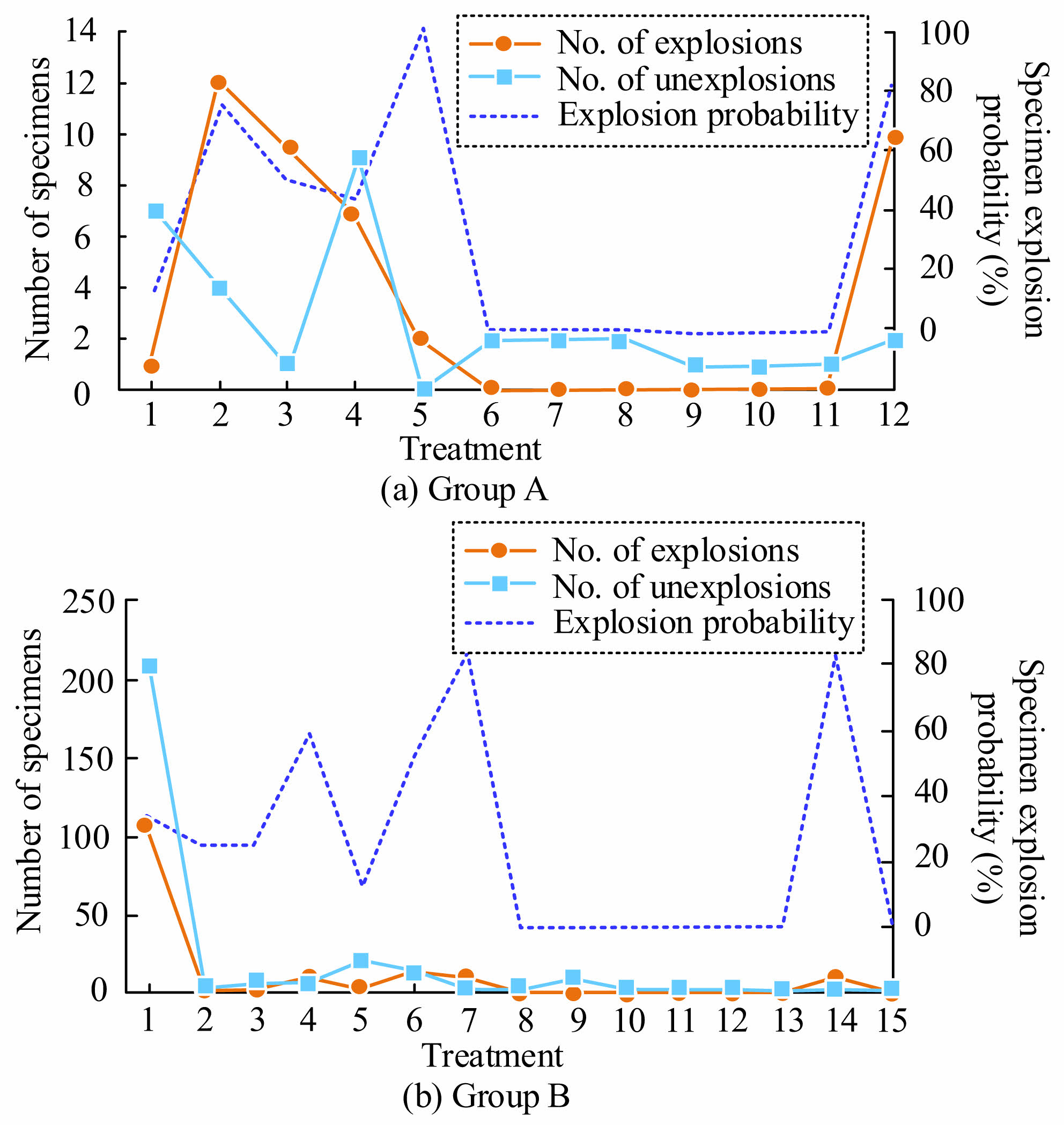
Based on the above dosage distribution, this study compares the effects of two groups of hybrid fibers on the HTE spalling of UHPC. The specific results are shown in Fig. 12. Fig. 12(a) shows the HTE situation of UHPC specimens with single PP fiber and mixed PP fiber + steel fiber. The relationship between fiber content in concrete specimens and HTE spalling fluctuates greatly and is complex. The HTE probability of the specimens doped with PP fiber alone is greatly superior to that of mixed fibers. When the PP fiber content of the specimens is all 0.90 kg/m3, the explosion probability of the single-doped fiber specimens is 100% higher than that of the mixed-doped fiber specimens (6, 7, 8). Comparing Fig. 12(b), the explosion probability of specimens with single steel fiber and mixed PP fiber + steel fiber is significantly higher than that with mixed fiber. This indicates that hybrid fibers can improve the blast resistance of UHPC, and the combined effect between different fibers increases the threshold range of concrete explosion, thereby reducing the risk of UHPC HTE spalling. This study further compares the relationship between the HTE spalling, CS, PP fiber content, and steel fiber content of two sizes of specimens.
Figure 13(a) shows the HTE peeling of a HUPC cube with a size of 100×100×100 mm. Compared to mixed fiber specimens, the peeling of single fiber content is more pronounced. With the mixing of the two fiber contents, the specimen shows almost no HTE peeling. In Fig. 13(b), the HTE spalling of HUPC cubes with dimensions of 150×150×150 mm shows that in the mixed fiber content specimens, the proportion of steel fibers is relatively low. When the proportion of PP fibers is high, the explosion spalling of the mixed specimens is more severe. Correspondingly, the CS of concrete also decreases with the increase of PP fiber content. The analysis results of two sizes of specimens show that when the CS is between 100-120 MPa, steel fiber 60 kg/m3, and PP fiber 2 kg/m3 are added, HUPC specimens can meet the requirements of engineering practice, and the high-temperature blast resistance performance of concrete is the best.
|
Fig. 8 Frequency distribution of ANN-1 model MC and water-cement ratio data |
|
Fig. 9 Frequency distribution of ANN-2 model MC and CS. |
|
Fig. 10 Prediction accuracy of PPM based on ANN algorithm. |
|
Fig. 11 Relationship between CS and MC and concrete explosive spalling in two concrete cubes. |
|
Fig. 12 Explosion of UHPC with single doped fibers and blended fibers. |
|
Fig. 13 Relationship between CS and fiber content and concrete explosive spalling in two concrete cubes. |
To explore the mechanism of UHPC HTE spalling and the influence of hybrid fibers on the intervention of UHPC anti-explosion performance, this study proposed a UHPC-HTE spalling prediction model based on the ANN algorithm. ANN-1 and ANN-2 models were constructed from the perspectives of concrete mix proportion and CS, and mixed fiber performance intervention tests were conducted. The prediction accuracy of the model based on the concrete mixture reached 96.87%, and the prediction accuracy of the CS model reached 88.22%. Blended fibers (PP fibers and steel fibers) have enhanced the high-temperature blast resistance of UHPC. Compared with the mixed fiber sample, the explosion probability of the single-doped PP fiber sample increased by 100%. The UHPC specimens doped with 60 kg/m³ steel fibers and 2 kg/m³ polypropylene fibers had the best high-temperature blast resistance performance when the CS was between 100 and 120 MPa. In addition, there was an inverse relationship between specimen size and spalling probability, with larger specimen size resulting in higher spalling probability.
Furthermore, the study's findings indicated that PP fibers undergo a phase transition at elevated temperatures, resulting in the formation of minute pores. These pores function as escape routes for water vapor, thereby reducing the internal vapor pressure. The steel fibers, on the other hand, provide additional tensile strength and toughness, enhancing the concrete's resistance to bursting. The probability of spalling of concrete is reduced by the hybrid fibers when they act synergistically. As the specimen size increases, the heat transfer path becomes longer, the internal heat build-up increases and the risk of spalling rises. These findings provide important theoretical support and engineering guidance for the application of UHPC in high-temperature environments.
However, this study exclusively examined the impact of mixed straight steel fibers and PP fibers on the HTE resistance of UHPC, omitting a comprehensive evaluation of the influence of steel fiber shape on the explosion resistance performance of concrete. Therefore, subsequent work will optimize the model and explore the role of fiber shape in the blast resistance performance of UHPC to weaken the negative impact of concrete HTE spalling.
This work was supported in part by Key research project of Zhejiang College of Security Technology “Research on the Residual Performance of Ultra-High Performance Concrete Affected by Fire” (Project Number:AF2025Z07), Basic scientific research project of Wenzhou Municipal Bureau of Science and Technology “Application Research of Ultra High Performance Concrete in Prefabricated Buildings” (Project Number: S2023034).
The authors report there are no competing interests to declare.
- 1. S. Banerji and V. Kodur, Fire Mater. 46[1] (2022) 287-301.
-

- 2. C. Oh, GLCE 1[3] (2023) 121-129.
-

- 3. I.Y. Hakeem, M. Amin, B.A. Abdelsalam, B.A. Tayeh, F. Althoey, and I.S. Agwa, Struct. Eng. Mech. 82[3] (2022) 295-312.
-

- 4. I. Almeshal, B.H. Abu Bakar, and B.A. Tayeh, Fire Technol. 58[5] (2022) 2589-2639.
-

- 5. R. Fürst, T. Vlach, M. Pokorný, and V. Mózer, Fire Technol. 58[1] (2022) 53-74.
-

- 6. S.M. Anas, M. Shariq, M. Alam, and M. Umair, Int. J. Prot. Struct. 13[4] (2022) 672-715.
-

- 7. A.T.G. Tapeh and M.Z. Naser, Fire Technol. 58[5] (2022) 2871-2898.
- 8. J.E.V.D. Merwe, J. S. Afr. Inst. Civ. Eng. 65[2] (2023) 2-9.
-

- 9. J.-C. Liu, L. Huang, Z. Chen, and H. Ye, Inter. J. Civ. Eng. 20[6] (2022) 639-660.
-

- 10. K. Iwama, Y. Kato, S. Baba, K. Higuchi, and K. Maekawa, J. Adv. Concr. Technol. 19[2] (2021) 106-117.
-

- 11. W. Wang, X. Liu, Y. Khan, Z. Ali, and A. Rahman, Def. Technol. 24[1] (2023) 326-339.
- 12. Q. Liao, X. Xe, and J. Yu, Struct. Concrete 23[6] (2022) 3601-3615.
-

- 13. Y. Mater, M. Kamel, A. Karam, and E. Bakhoum, Constr. Innov. 23[2] (2023) 340-359.
-

- 14. A. Seitllari and M. Naser, Comput. Concrete 24[3] (2019) 271-282.
-

- 15. H. Moayedi, Steel Compos. Struct. 44[6] (2022) 867-882.
- 16. G. Li, Y. Xue, C. Qu, D. Qiu, P. Wang, and Q. Liu, Environ. Sci. Pollut. Res. 30[12] (2023) 33960-33973.
-

- 17. H.K. Shin, H.Y. Kim, and S.H. Lee, CMC‑Comp. Mater. Con. 70[3] (2022) 5059-5071.
-

- 18. J. Choi, J. Jeong, X. Zhu, J. Kim, B.K. Kang, Q. Wang, B.-I. Park, S. Lee, J. Kim, H. Kim, J. Yoo, G.-C. Yi, D.-S. Lee, J. Kim, S. Hong, M.J. Kim, and Y.J. Hong, ACS Nano 17[21] (2023) 21678-21689.
-

- 19. F. He, Y. Cao, Y. Liu, J. Li, J. Wang, B. Zhang, and N. Dong, Ceram. Int. 49[3] (2023) 5335-5344.
-

- 20. K. Zhao, Y. Lai, Z. He, W. Liu, R. Zhao, Y. Wang, X. Tian, and J. Nie, Process Saf. Environ. 174[1] (2023) 983-996.
-

- 21. A. Kilani, C. Fapohunda, O. Adeleke, and C. Metiboba, Res. Eng. Struct. Mater. 8[2] (2022) 307-336.
-

- 22. U. Pulkit and S.D. Adhikary, Struct. Concrete 23[4] (2022) 1995-2014.
-

- 23. S.M. Anas, M. Alam, S. Akram, R. Tahzeeb, M. Shariq, and M. Umair, Int. J. Sustain. Mater. Struct. Syst. 6[1] (2022) 61-108.
-

- 24. A.I. Taloba, Alex. Eng. J. 61[12] (2022) 9287-9295.
- 25. Q. Shao, Soft Comput. 28[4] (2024) 3633-3648.
-

- 26. Q. Ni and M. Zhang, Appl. Intell. 52[13] (2022) 15026-15039.
-

- 27. S.F. Ahmed, M.S.B. Alam, M. Hassan, M.R. Rozbu, T. Ishtiak, N. Rafa, M. Mofijur, A.B.M.S. Ali, and A.H. Gandomi, Artif. Intell. Rev. 56[11] (2023) 13521-13617.
-

- 28. S. Lu, S. Liu, P. Hou, B. Yang, M. Liu, L. Yin, and W. Zheng, Comput. Model. Eng. Sci. 136[1] (2023) 363-379.
-

- 29. M. Chen, H. Jiang, W. Liao, and T. Zhao, Inf. Inference 11[4] (2022) 1203-1253.
- 30. S.S. Atamanalp, J. Laparoendosc. Adv. Surg. 32[7] (2022) 763-767.
-

- 31. Y. Wang, Z. Xiao, and G. Cao, J. Vibroeng. 24[4] (2022) 666-678.
-

- 32. J.Z. Deng, J.S. Chan, A.L. Potter, Y.-W. Chen, H.S. Sandhu, FRCSC, N. Panda, D.C. Chang, and C.-F. Yang, Ann Surg. 275[2] (2022) 242-246.
-

 This Article
This Article
-
2025; 26(4): 535-546
Published on Aug 31, 2025
- 10.36410/jcpr.2025.26.4.535
- Received on Nov 21, 2024
- Revised on Feb 17, 2025
- Accepted on Mar 11, 2025
 Services
Services
- Abstract
introduction
ppm based on ann algorithm and mixed fiber performance intervention experiment
verification of ppm based on ann algorithm and intervention analysis of hybrid fiber performance
conclusion
- Funding
- Disclosure Statement
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- Chenhao Xu
-
Department of Intelligent Architecture, Zhejiang College of Security Technology, Wenzhou 325016, China
Tel : 18005779765 - E-mail: chenhaoxu258@outlook.com






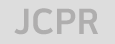 Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.
Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.