An experimental study was conducted to optimize both the surface roughness and material removal rate in the end milling process of Al-6063 alloy. Grey relational coefficients determined by using grey relational normalized formula. GRG values are analyzed and optimum level of process parameters that lead to highest GRG value indicates the overall performance of the output characteristics. ANOVA analysis is performed to determine the influencing parameter in end milling process. The optimum process parameters are determined using fuzzy logic and grey relational grade and it is found that grey relational grade is improved and provides minimum surface roughness and maximum material removal rate.

Keywords: ANOVA, End milling, Fuzzy logics, Grey relation analysis, MRR, Surface roughness.

The basic material removal process used in the industries is milling process since it find- applications in several sectors [2]. The raw materials are draw into the correct dimensions by a controlled material-removal process. Surface roughness is theoretical quality indicator for machined surfaces [1]. Surface roughness plays a crucial role in machining operations as it is a critical technical requirement for mechanical products. Attaining the desired surface quality is of utmost importance for ensuring the optimal functional behavior of a part [3]. The micro-end-mill issued for the process of machining of Aluminium alloy in this work [11]. Studied the friction stir processed GFRP plates subjected to milling. Response surface methodology is used to correlate the relationship between the input variables and the response variables considered in the machining process [6]. To perform theoretical and mathematical calculated the results used in modelling of end milling process of Al alloy [4]. Surface roughness significantly decreases the fatigue life of aluminium alloys. This is primarily because surface roughness results in local stress concentration, which leads to the initiation and propagation of fatigue cracks. Therefore, minimizing surface roughness is crucial to improve the fatigue performance and overall durability of aluminum alloy components [9]. Investigated the effort of best machining conditions for raising the output and realizing prime quality through increase removal rate and improve surface quality [13]. Cutting conditions raised in the micro milling process are connected to machining directly [5, 7]. According to the [10], dynamic stability loss is resulted from low feed rates selected during micro milling and this favours the elastic deformation of the work piece. GRA calculated by using a categorized into two types namely Lower the better, higher the better criterion [15]. The manufacturing process parameters can be optimized through various commonly used offline experimental techniques.
When machining an aluminum block with a high-speed steel end mill cutter, one can employ these techniques To achieve the optimal cutting parameters for micro-end milling operations [8, 14]. General computing modules such as Mat Lab implement popular fuzzy methods, like the so-called “Mamdani fuzzy inference” (Mat Lab 2018) [12]. Applications of fuzzy logic are numerous. Fuzzification is the process of accepting the inputs and processing these inputs to next levels. During the fuzzification process, the input quantity, which can be either digitally precise or imprecise, is transformed into linguistic terms. This translation allows the data to be processed by an inference mechanism that applies predefined rules. The inference mechanism then produces an output in linguistic form. To convert the linguistic output back into numerical form, representing normal data, it undergoes a defuzzification process. This process ensures that the final output is in a numerical format [18]. Multi objective optimization using Taguchi technique is employed for determining the optimal process parameters while machining [16, 17]. Multi criteria decision making is used to find the optimum machining process parameters for Inconel 718 [19]. Optimum selection of process parameters in EN 31Alloy steel for surface roughness and MRR using Taguchi method provides the best results [20]. Several researcher used newer optimization techniques for new machining approaches and improving solar collector performances [21-23].
AL6063 finds several applications in architectural applications, agriculture, irrigation, transportations etc., In industries AL6063 is useful for manufacturing components for vehicles, trailers, retail fixtures, door frames etc. Grey-fuzzy optimization, combining grey system theory and fuzzy logic, is a powerful approach for optimizing industrial automation processes. Grey system theory deals with systems where information is incomplete, uncertain, or fuzzy. It provides tools to analyze and model such systems when precise data is unavailable. The industrial applications of Grey fuzzy optimization are predominant in Optimization of CNC turning, Process parameter optimization, Welding process optimization, Journal bearing optimization and so on.

Machining Parameter Selection
The experiment involved using an HSS end mill cutter with a diameter of 12 mm and a length of 75 mm. Multiple trial runs were used to select the machining parameters, including feed rate, speed, and depth of cut, in order to assess their effects on surface roughness and material removal rate. A wrought plate of AL 6063 high strength aluminium alloy, with dimensions of 50 mm length, 50 mm width, and 16 mm thickness, was used for the experimentation. While turning operation, the most influential turning process parameters are depth of cut, cutting speed and feed rate. In this work turning of Al6063 is performed and hence these process parameters are selected. Material removal rate and surface roughness were measured as the responses to the variations in the process parameters. Surface roughness and material removal rate are the important responses in optimizing the process parameters while machining AL6063 alloy. They are highly responsible for the quality and efficiency of the process. The finish of the work piece is dependable on the surface finish and if the surface finish is good, the aesthetic appearance of the work piece is improved to a great extent. Also the material removal rate directly impacts on procution time and cost and it improves the productivity.
18 experiments as per Taguchi design are conducted. For each combination of design, three experiments are conducted to measure the surface roughness and material removal rate. Average of these three values are finally recorded as the experimental data. A typical end mill cutter used in this work is shown in the Fig. 1 and experimental set up is shown in Fig. 2.
Grey relational analysis
Grey relational grade optimizes the multi response characteristics into a single response characteristic. In this work the multi response optimization for maximizing the material removal rate and minimizing the surface roughness are converted to a single performance index. GRG values are analyzed and optimum level of process parameters that lead to highest GRG value indicates the overall performance of the output characteristics. A Grey-fuzzy relation grade combines the benefits of grey relational analysis and fuzzy logic in multi-response optimization problems. The complex performance characteristics are analyzed by converting the grey relational coefficients of multiple responses into a single grey-fuzzy grade.
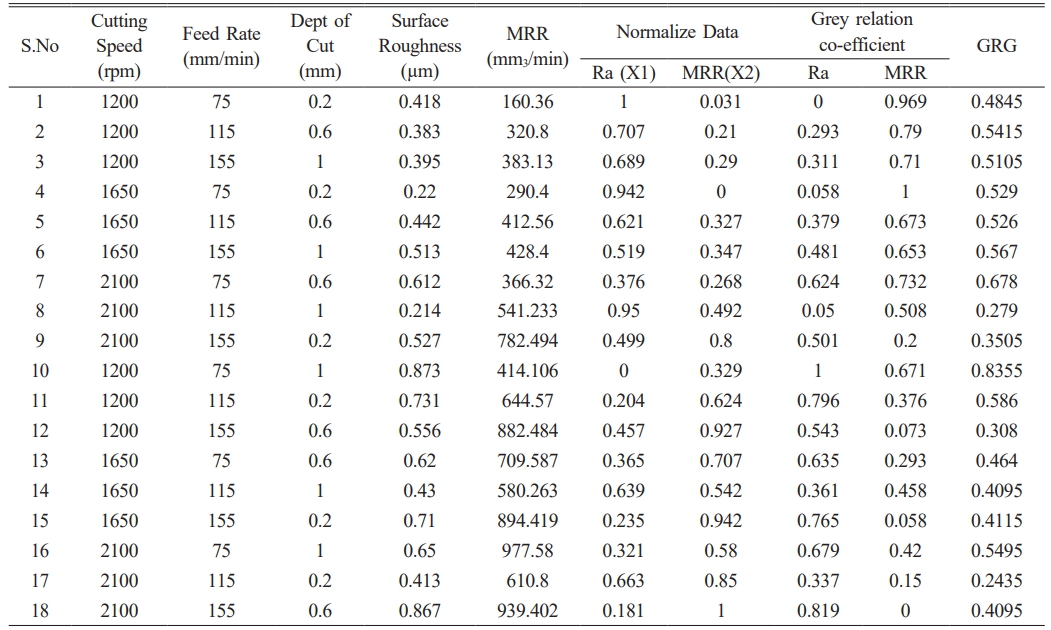
The optimum machining parameters are evaluated using Grey relational analysis. “Smaller- the better” is employed to surface roughness and “large the better” condition is employed to material removal rate, and also the original sequence is normalized. An ideal sequence is x0(k) (k=1, 2….18). Relationship is obtained after data pre-processing using Grey relational coefficient. Using the maximum number of normalized values, the deviation sequence is evaluated regardless of responses, trials and replications. Table 1 presents the experimental values recorded for surface roughness and material removal rate and the grey relation grade for surface roughness and material removal rate. Grey relational is given by the equation Identification coefficient which is taken as 0.5 generally in all cases.

Fuzzy inference system
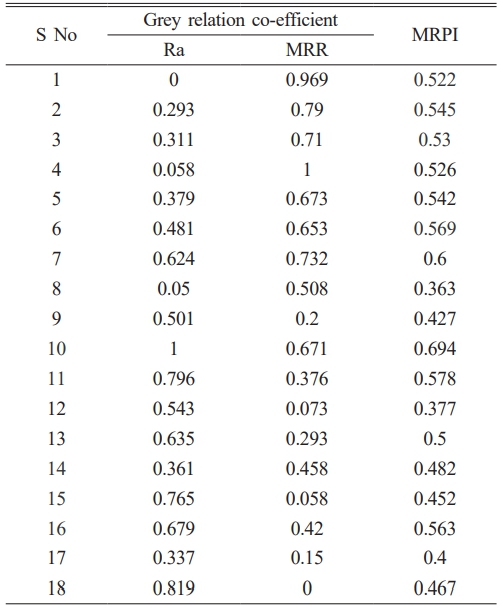
The Mamdani fuzzy inference system has been chosen for this study. The input parameters utilized are the Grey relational coefficient for surface roughness (Ra) and Material Removal Rate (MRR), while the Multi-Response Performance Index (MRPI) is considered as the output parameter.
For the fuzzification process, the linguistic variables of low (L), medium (M), and high (H) are employed for the input factors. Similarly, the output variable is represented by the linguistic variables of very low (VL), low (L), medium (M), high (H), and very high (VH). Surface plots that illustrate the variations in grey relation coefficients provide a visual representation of how the grey relation coefficients change with different combinations of input factors.

Grey Relational Grade
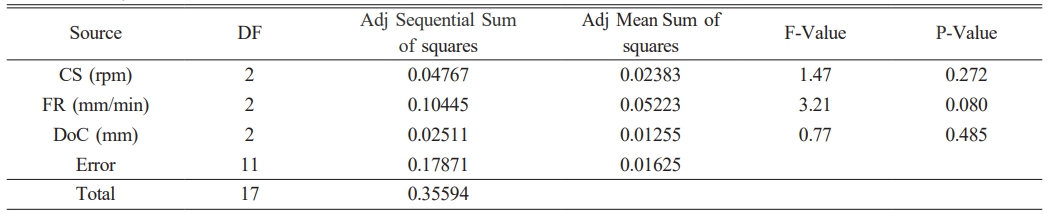
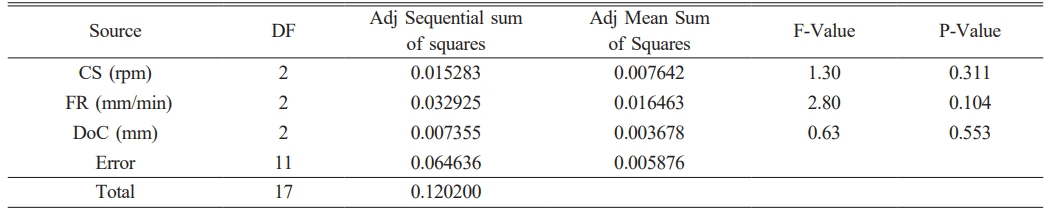
The ANOVA for GRG is shown in Table 3 describes that the percentage of the cutting speed is 27.8 and percentage of the feed is 08.2 and the percentage of the depth of cut is 48.3. From this table it is evident that the dominating parameters in the determination of optimal cutting parameters, the depth of cut plays a major role When compared to the other parameters. Also the percentage of error is determined as 5.6. The GRG Values for the experiments 1-6, 7-12 and13-18 respectively are used for calculating the grey relational grade values for the level 1 parameters.
Analysis of variance for GFRG
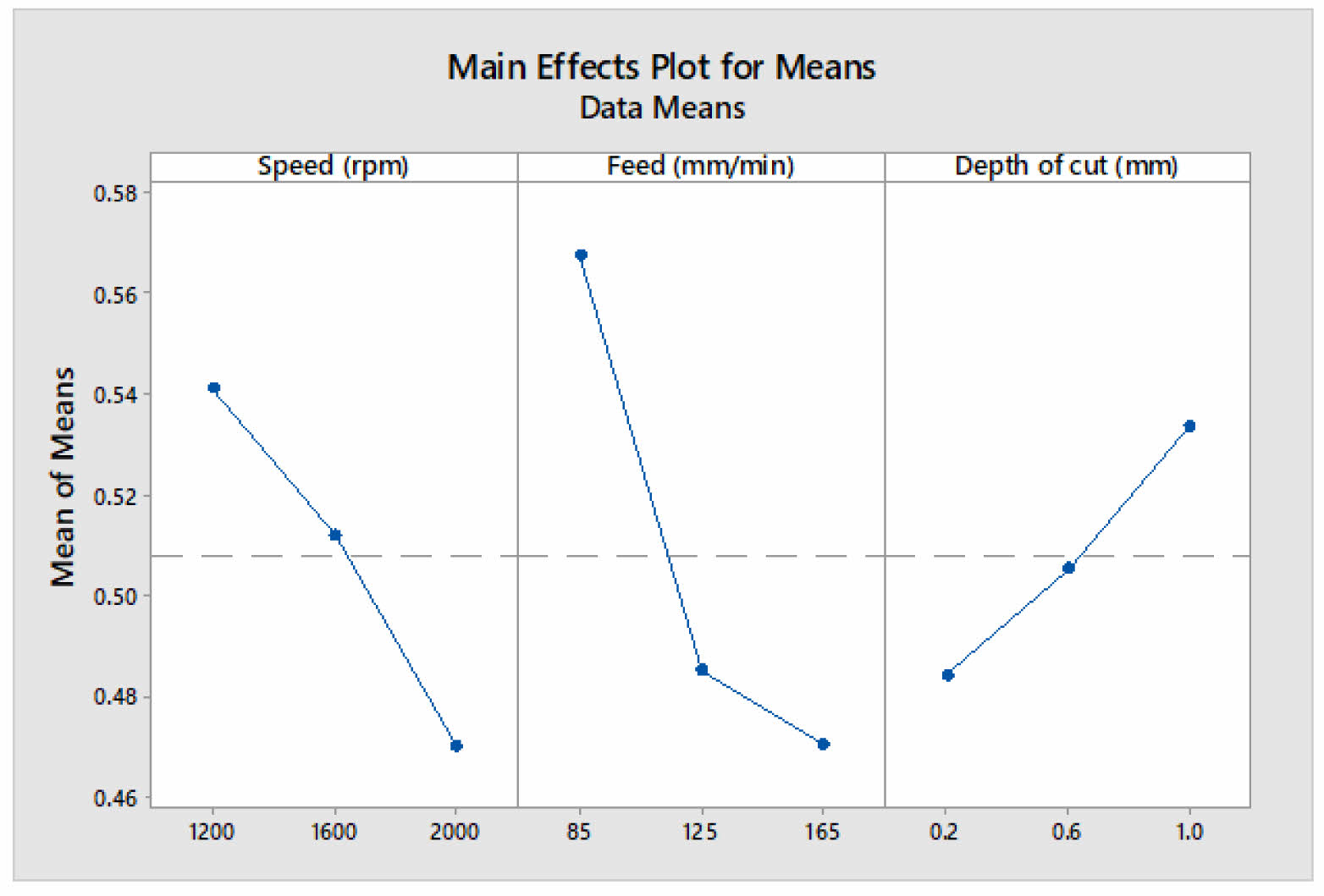
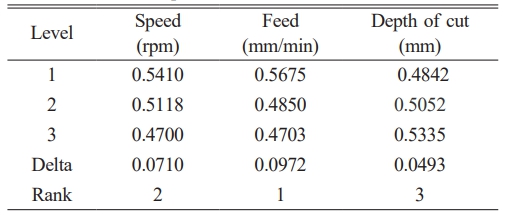
Table 4 represents the ANOVA result for grey fuzzy reasoning grade. The percentage of contributions of the process parameters in milling operations can be determined by Analysis of variance. The fuzzy logic techniques are useful in determining the grey fuzzy reasoning grade. Table 5 represents the Mean response values of grey fuzzy reasoning grade values. The optimized values are; speed 1250 rpm (A1), Feed 75 mm/min (B1), depth of cut of 1.0 mm (C3). In the most significant factor is cutting speed 31.10%, followed by the depth of cut 55.3% and then feed rate 10.4% and then error is 4.93%. Fig. 3 represents the mean effects plot for means for GFRG. 18 set of the framed rules are developed using grey fuzzy approach and Grey-fuzzy reasoning grade are evaluated and grey relational grades are obtained and it shows an improvement when compared grey fuzzy reasoning grade thereby reducing the fuzziness.

By comparing the optimal process parameter levels, it was found that fuzzy logic outperformed grey relational grade. The grey relation grade improved from 0.604 to 0.695, while FGRA (Fuzzy Grey Relational Analysis) also improved from 0.578 to 0.629. This approach led to significant improvements in both surface roughness and material removal rate values. The experimental values were calculated to identify the optimal levels of input process parameters. The best and optimized levels obtained were a speed of 1200 rpm, a feed rate of 75 mm/min, and a depth of cut of 1.0 mm.