High-speed motorized spindles with grease-lubricated bearings encounter significant temperature rise and vibration, severely affecting their operational accuracy. This paper proposes substituting traditional metal bearings with full-ceramic bearings to tackle this issue, given the superior material properties of ceramic. A quasi-static model was developed to analyze the behavior of full-ceramic bearings under varying speeds and preload levels, focusing on parameters such as spin-roll ratio. Subsequently, experimental tests were conducted to compare the temperature rise and vibration characteristics of full-ceramic, metal, and hybrid bearings under varying conditions, and the data were analyzed in conjunction with the quasi-static model results. The findings indicate that the dynamic and thermal characteristics of bearings generally increase with speed. While metal bearings exhibit an initial decrease followed by an increase in performance with preload increases, full-ceramic and hybrid bearings show similar trends, with performance heavily influenced by preload. The behavior of full-ceramic bearings is the best at varying speeds and preload levels, ensuring smoother machinery operation. The study provides valuable insights for the practical exertion of full-ceramic bearings in high-speed motorized spindles.

Keywords: High-speed motorized spindle, Full-ceramic bearings, Pseudo-statics method, Temperature rise characteristics, Vibration characteristics.

Owing to the continuous progress in the mechanical industry, high-speed motorized spindles have been extensively adopted in various fields, including aerospace, precision machinery, automotive manufacturing, and other industries [1-3]. As a critical component of high-motorized spindles, rolling bearings are subjected to increasingly demanding performance requirements [4-6]. Among these requirements, temperature rise and vibration have become key indicators for evaluating bearing performance, primarily at high-speed conditions [7]. Excessive vibration and temperature rise, significantly reducing running accuracy and potentially to cause damage, are the primary causes of most bearing failures. Traditional grease-lubricated metal bearings often encounter these challenges due to their material characteristics [8-10]. On the contrary, full-ceramic bearings possess advantages, including a low friction coefficient, low density, and self-lubricating properties, which enable stable operation under high-speed conditions [11]. Given the growing demand for high-speed motorized spindles and the limitations of traditional metal bearings, it is crucial to investigate the performance of full-ceramic bearings under high-speed conditions with grease lubrication. Besides material properties, preload also significantly influences bearing temperature rise and vibration. Applying a suitable preload to the bearing ensures the ball and raceway have continuous contact, which enhances rotational accuracy, and reduces ball spin and gyroscopic rotation. These effects lower vibration and temperature rise, improving bearing performance [12, 13]. However, excessive preload can cause an increase in contact load and contact deformation, leading to intensified bearing vibration and temperature rise [14]. This highlights the importance of selecting an appropriate preload level to achieve optimal bearing performance.
Researchers have extensively explored the impact of preload levels and speeds on bearings' quasi-static properties, dynamic and thermal characteristics in recent years. Hikmet et al. [15] performed both theoretical and experimental analyses to examine the vibration characteristics of a rotating mechanical system utilizing bearings under varying preload levels. Chen et al. [16] analyzed the impact of bearing arrangement, preload configuration, and real-time load control on bearing performance, focusing on the roles of centrifugal force and thermal effects on load distribution. Fang et al. [17] developed a thermodynamic coupling model for a high-speed spindle-bearing system using multi-degree-of-freedom finite element and thermal grid methods, investigating the effects of temperature rise and thermal deformation on its dynamic behavior. Aydin et al. [18] studied the impact of preload on the modal properties of shaft-bearing systems incorporating double-row angular contact ball bearings. Li et al. [19] introduced a novel non-uniform preload approach for spindle-bearing systems, investigating its impact on both static and dynamic performance through combined theoretical and experimental analyses. Xu et al. [20] developed an analytical approach to precisely identify the optimal preload across various speed ranges. Zhang et al. [21] introduced a pseudo-dynamic model to examine the load distribution in ball bearings under arbitrary preload levels by evaluating the ball-raceway contact state. Zhang et al. [22] introduced a dynamic wear simulation framework to analyze the impact of varying preloading methods and preload variations due to wear on the lifespan of bearings. Zhang et al. [23] analyzed the effects of combined bearing preload and angular misalignment on the fatigue life of ball bearings and bearing-shaft systems.
For full-ceramic bearings. Wang et al. [24] investigated temperature rise and vibration characteristics across three bearings under varying lubrication modes. Previous studies [25, 26] examined vibration and temperature rise behavior of full-ceramic bearings under low-temperature conditions with varying speeds and loads. Sun et al. [27] studied the effects of different cage materials on temperature rise and vibration of full-ceramic ball bearings under dry friction. Li et al. [28] discussed the effect of raceway surface morphology on the temperature rise characteristics of full-ceramic bearings under solid lubrication. In previous work [29, 30], the researchers carried out experimental research on the temperature rise of full-ceramic bearings under different lubrication conditions, and analyzed the influence of operating parameters on the lubricating oil film with simulation.
Numerous researchers have analyzed the behavior of bearings under varying preload levels and speeds. However, the current research on full-ceramic bearings has achieved some results at low temperature, dry friction, high speed, performance comparison and so on, it still lack of the effect of preload on the dynamic and thermal characteristics of full-ceramic bearings and the comparison of different bearing performance under variable preload. The primary focus of this research is the bearing mechanism in high-speed motorized spindles. This study systematically investigates the effects of rotational speeds and preload levels on the vibration and thermal behavior of full-ceramic bearings, employing pseudo-static analysis combined with experimental research of vibration and thermal characteristics. The test results demonstrate the advantages of full-ceramic bearings, particularly their reduced vibration and temperature rise, which improves machining accuracy in precision equipment such as CNC machining tools by impoving motorized spindle performance. Furthermore, the full-ceramic bearings' exceptional thermal stability mitigates lubricant thermal degradation risks during high-speed operation, extending lubrication replacement cycle and reducing cooling system energy consumption.
Pseudo-static model
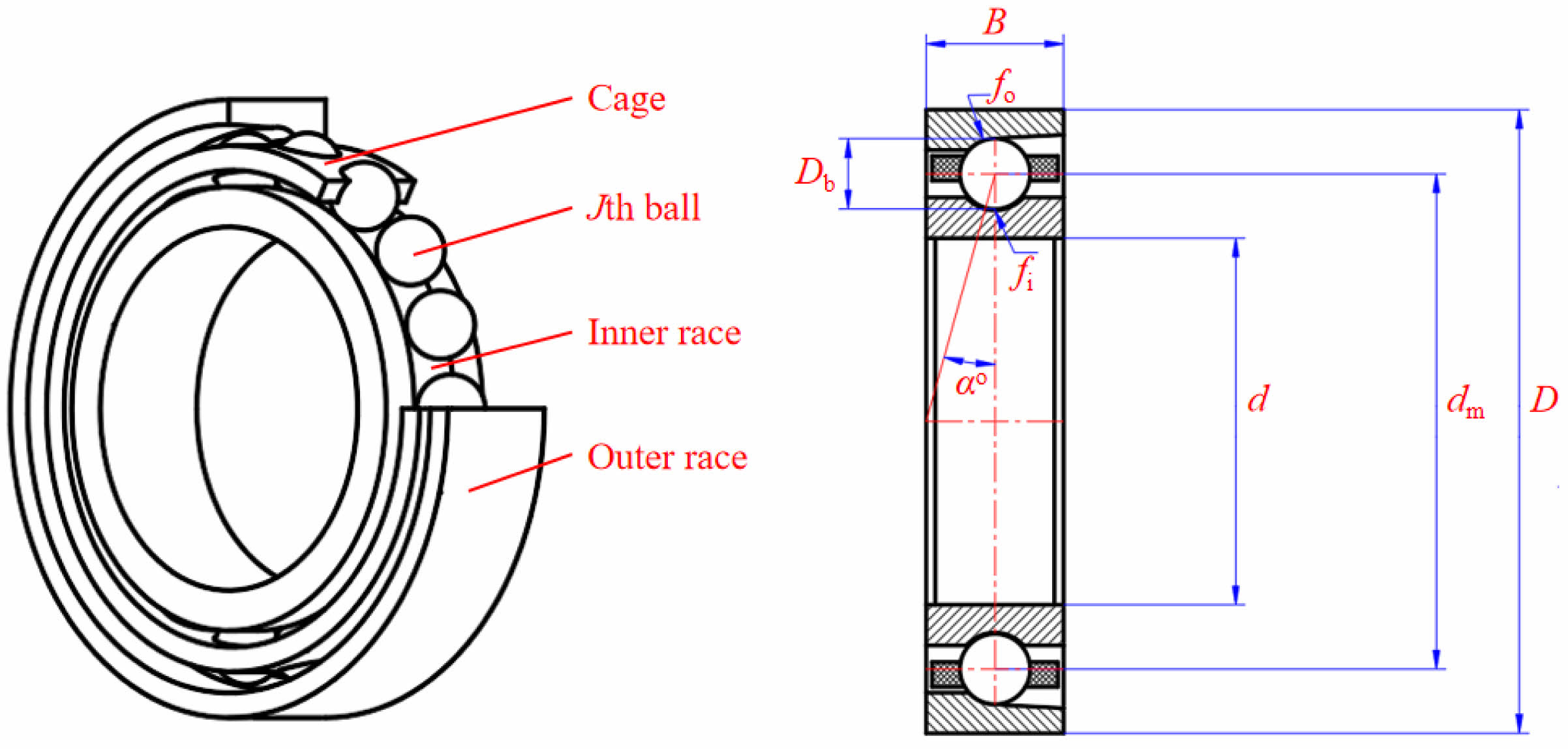
The quasi-static properties of bearings can influence their performance. To explore this influence, we established a quasi-static model for full-ceramic bearings. Fig. 1 illustrates the design layout of the 7008C bearing, and Table 1 provides its specific design parameters.
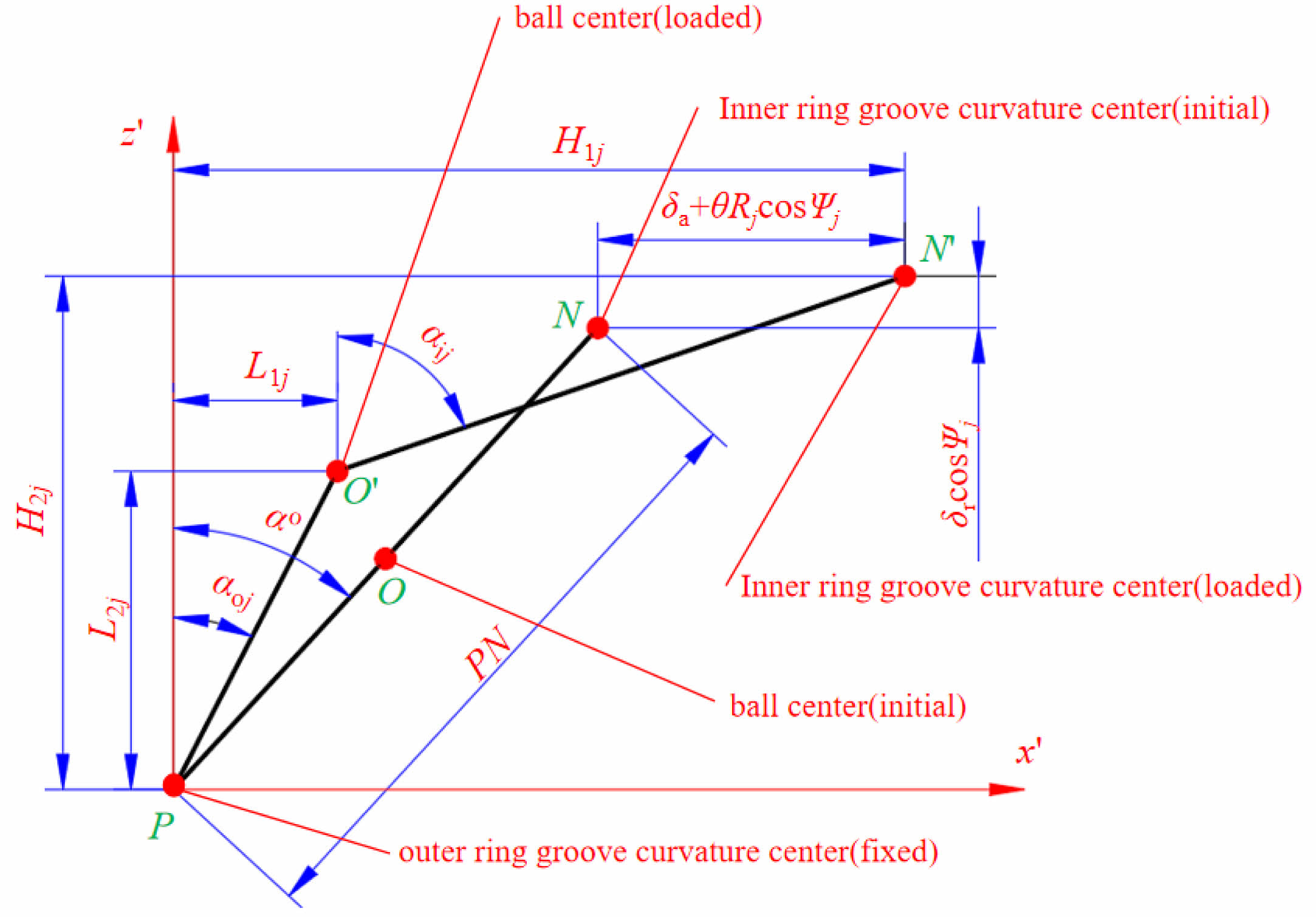
The curvature center (Fig. 2) offset of raceway grooves (inter and outer raceway) at specified angular location ψ_j, determines the sphere's final center position:




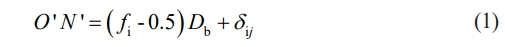
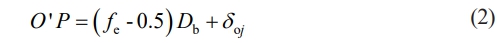
where j stands for the j-th ball, δ_ij and δ_oj represent deformation at ball-inner/outer ring raceways contact at the Angle position ψ_j.
The relative curvature center spacing of inner/outer raceway (axial and radial) channels is [31]:



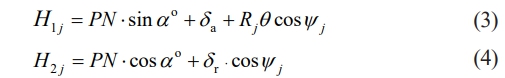
where δ_a and δ_r correspond to orthogonal displacement components of raceways, α^o is the unloaded contact angle, and θ is the relative tilt angle of rings.
At angular location ψ_j, the effective contact angle is:



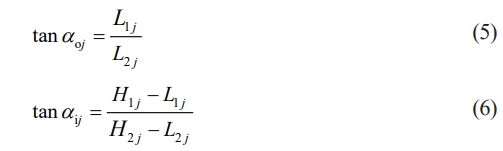
The sphere center position change with the geometric relationship is derived as [32]:



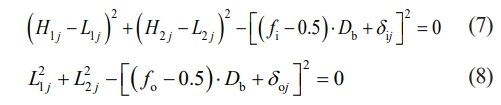
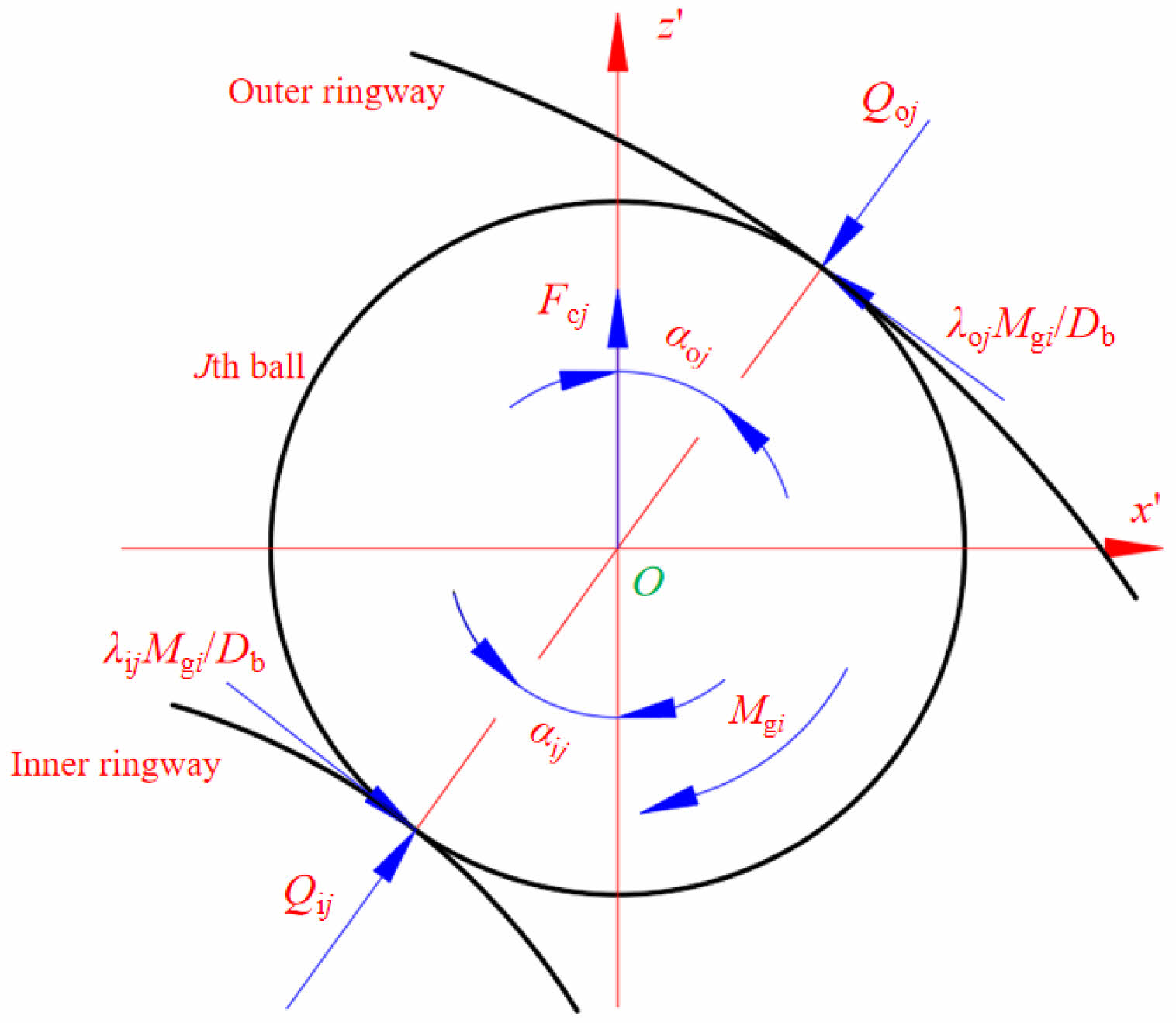
The force on the ball (Fig. 3), regarding the bearing axis and ball center plane at the angle ψ_j, in the case of slight non-coplanar friction.
The force equilibrium conditions of the ball along orthogonal axes are [31] :



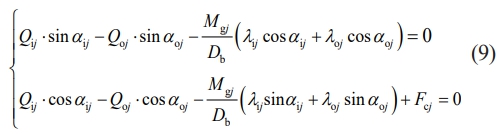
where, M_gj represents the gyroscopic moment of the ball, F_cj represents the centrifugal force, δ_ij and δ_oj correspond to the interfacial normal load at ball-rings contacts. For external channel control, λ_ij=0, λ_oj=0. For non-external channel control, λ_ij=1, λ_oj=1.



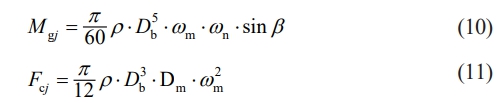
where ρ represents the ball density, ω_m and ω_n are the ball’s rotational and circular velocities, and β is:



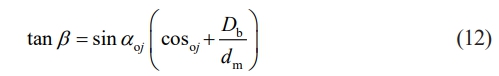
The spin-roll ratio at the rolling element-inner ring contact is:



Hertz's contact theory defines the deformation-stress relationship in rolling bearings as:



The ball bearing's deformation-load coefficient K is derived as [33]:



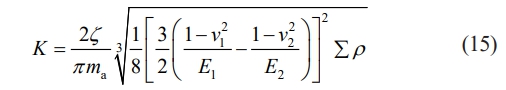
where ζ denotes the complete first-kind elliptic integral, m_a is the ellipse eccentricity coefficient, v₁ and v₂ are the Poisson ratio of the materials (ball and raceway), E₁ (ball) and E₂ (raceway) are the respective elastic moduli of the contacting materials, and ∑ρ is the effective principal curvature at the contact zone.
The contact relationship between applied load and deformation at ball-raceway interfaces is:



The bearing's inner ring force balance equation is [32]:



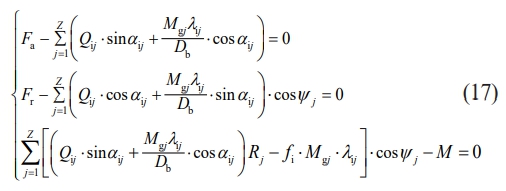
where the bearing experiences simultaneous axial (F_a), radial (F_r), and moment (M) loading.

The experimental study investigated three types bearings: the full-ceramic bearings, fabricated entirely from Si₃N₄ for both inner/outer rings and balls; the hybrid bearing, constructed with GCr15 rings combined with Si₃N₄ ceramic balls; and the metal bearing, exclusively manufactured from GCr15 for both rings and balls. All bearings were equipped with phenolic resin cages, with rings precision meeting P4 grade and balls complying with G5 grade precision. The detailed parameters of materials are summarized in Table 2.
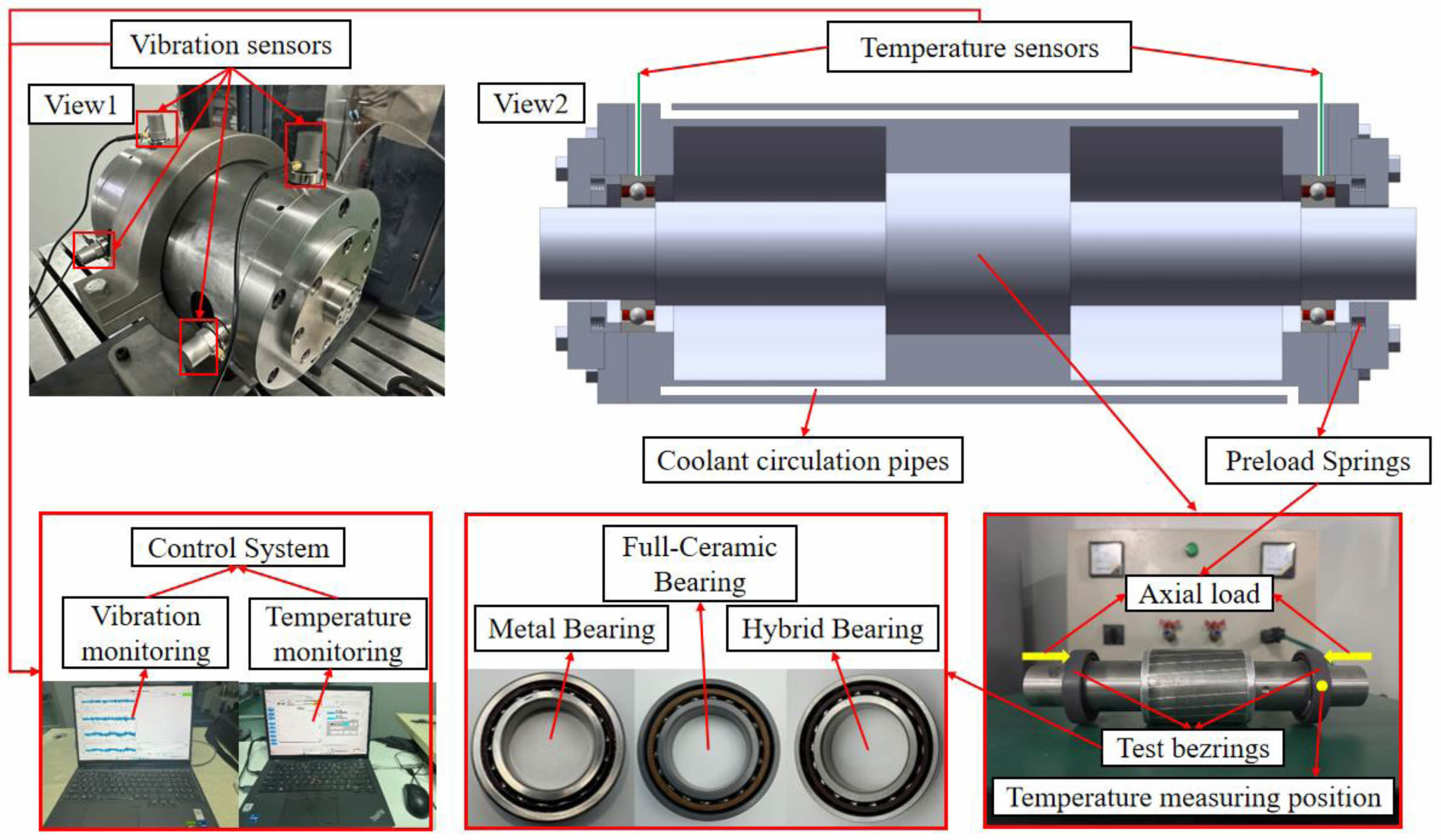
The test platform integrates a motorized high-speed spindle system with multi-parameter monitoring capabilities. The specific structure is shown in Fig. 4, and includes a temperature monitoring system for measuring the outer ring temperature of bearings and a Chengtec CT9204 four-channel vibration acceleration sensor coupled with a signal acquisition instrument, along with a motorized spindle, cooling equipment, and a control system, all maintained under consistent operational conditions with coolant thermal regulation at 17 ℃ to ensure thermal stability throughout the testing process. The preload application mechanism is shown in Fig. 5, the preloading method is constant pressure preloading and the preload is provided for the bearing by pressing the spring. Before the experiment, we measured each spring delivers 20 N ± 0.5 N at design compression state.
The previous research [34] established through theoretical analysis that angular contact bearings exhibit
optimal preload ranges for thermal performance. Accordingly, we selected four preloads: 240 N, 320 N, 400 N, and 480 N. The experiments were conducted at an ambient temperature of 25 ℃, applying varying preload levels to three distinct bearing types across a range of speeds. Each study group was run for 60 minutes, during which the temperature and vibration characteristics of the bearings were meticulously recorded. A comprehensive summary of the study is presented in Table 3.

Full-ceramic bearing pseudo-static results
The amount of the bearing parameters, such as spin-roll ratio, contact load and deformation, which can affect the vibration and temperature rise. To explore the consequence of speed and preload on the spin-roll ratio and other performance parameters in full-ceramic bearings, we employ the pseudo-static theory to analyze the state of the bearing under pseudo-static conditions.
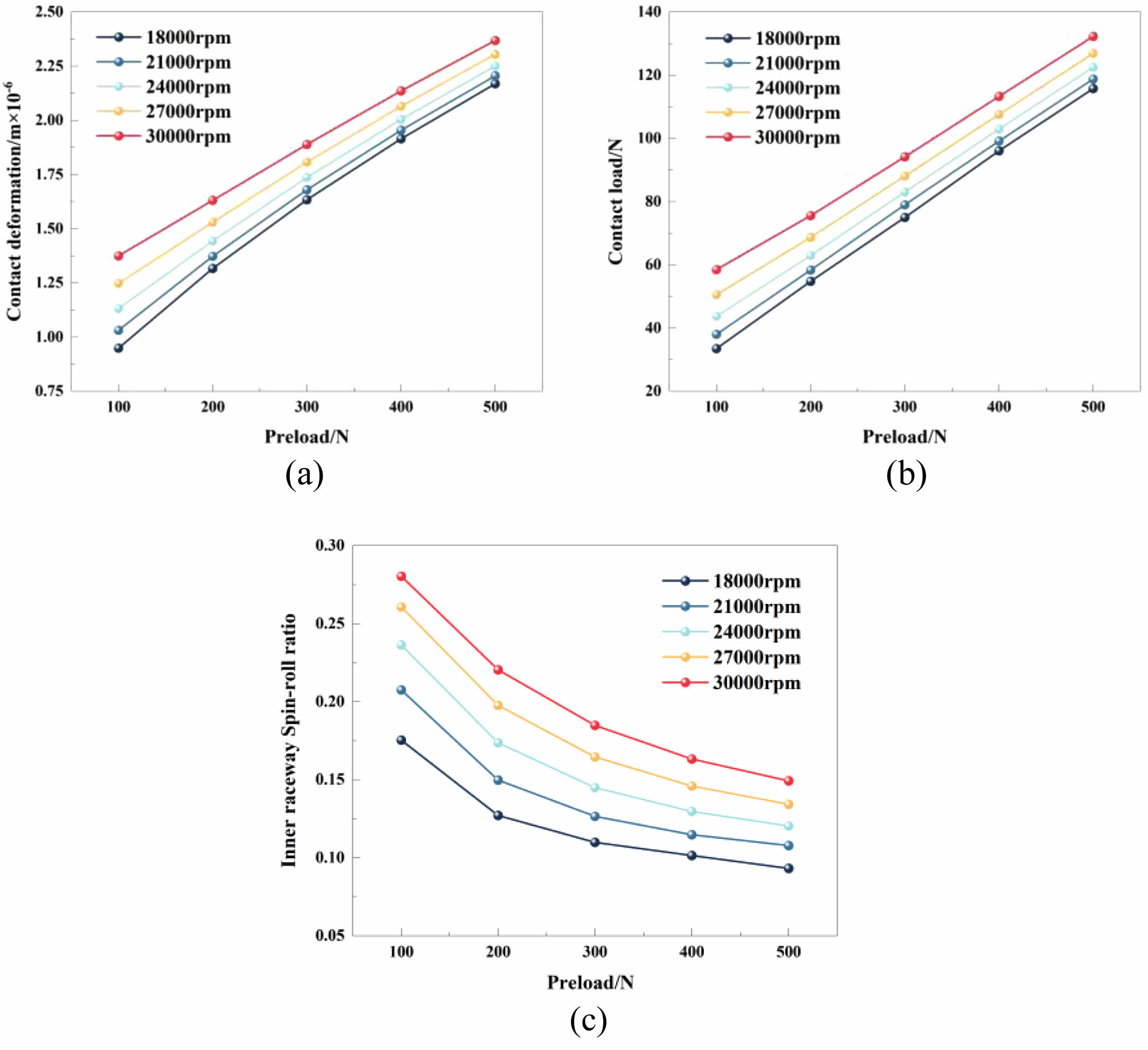
As shown in Fig. 6(a), the spin-roll ratio increases with speed but decreases with preload. When the preload reaches 300 N, the downward trend gradually slows down. For instance, at 30,000 rpm, the spin-roll ratio decreases from 0.28 to 0.19 as the preload increases from 100 N to 300 N. However, when the preload further increases from 300 N to 500 N, the ratio only drops to 0.15. Furthermore, excessive preload does not significantly reduce the spin-roll ratio. The changes in spin-roll ratio exhibit a similar trend with speed increases, but it consistently decreases as the preload increases. A higher spin-roll ratio indicates that spin motion at the ball-raceway contact point contributes more significantly to the overall movement. However, an excessively high spin-roll ratio can disrupt the equilibrium at the contact point, leading to increased vibration, friction, and heat generation, which negatively impact bearing performance. Therefore, controlling the spin-roll ratio at an appropriate value is intuitively important.
As seen in Fig. 6(b), the contact deformation increases with speed and preload. At 30,000 rpm, as the preload increases from 100 N to 500 N, the contact deformation rises from 1.375×10^-6 m to 2.369×10^-6 m. Similarly, when the speed increased from 18,000 rpm to 30,000 rpm, the contact deformation rose from 2.169×10^-6 m to 2.369
×10^-6 m at a 500 N preload. These results indicate that both higher speeds and preload levels result in increased contact deformation; the preload has a greater impact on contact deformation. As the preload increases, the impact of speed on contact deformation gradually diminishes. For instance, the deformation amount from 18,000 rpm to 30,000 rpm is 0.4261×10^-6 m at a 100 N preload but reduces to 0.2×10^-6 m at a 500 N preload. Elevated contact deformation reflects greater elastic deformation at the contact point, which can disrupt the uniformity of load distribution and compromise the integrity of the oil film. The uniformity of load distribution causes localized stress concentrations, resulting in the bearing failure. Additionally, the damage to the oil film causes direct contact between materials, resulting in greater heating.
As depicted in Fig. 6(c), show that both speed and preload lead to a continuous increase in contact load. The effect of preload on contact load shows a linear relationship. For example, at 30,000 rpm, the preload increases from 100 N to 500 N, and the contact load increases from 58.5 N to 132.3 N with an average increase of approximately 18 N for every 100 N preload increment. Similarly, when the speed increases from 18,000 rpm to 30,000 rpm, the contact load change is 24.97 N at a 100 N preload but reduces to 16.5 N at a 500 N preload. These results indicate that the influence of speed on contact load decreases as the preload increases. A higher contact load amplifies friction at the ball-raceway interface, which can significantly affect bearing performance by increasing heat generation and accelerating wear. This highlights the importance of optimizing preload to minimize adverse effects on bearing operation, ensuring stable performance and life.
Impact of speed and preload on vibration behavior
Impact of speed and preload on vibration acceleration
Bearing vibration is typically evaluated using the root mean square (RMS) value, kurtosis, and peak factor. In this study, we use the RMS value as the primary metric to assess vibration levels.The test device recorded bearing time-domain data and calculated the RMS of vibration acceleration over 0.1-second intervals under various conditions. The results are shown in Fig. 7. The RMS value is calculated using the following formula:



where N represents the total data points, and x_i denotes the vibration acceleration magnitude of the i-th point.
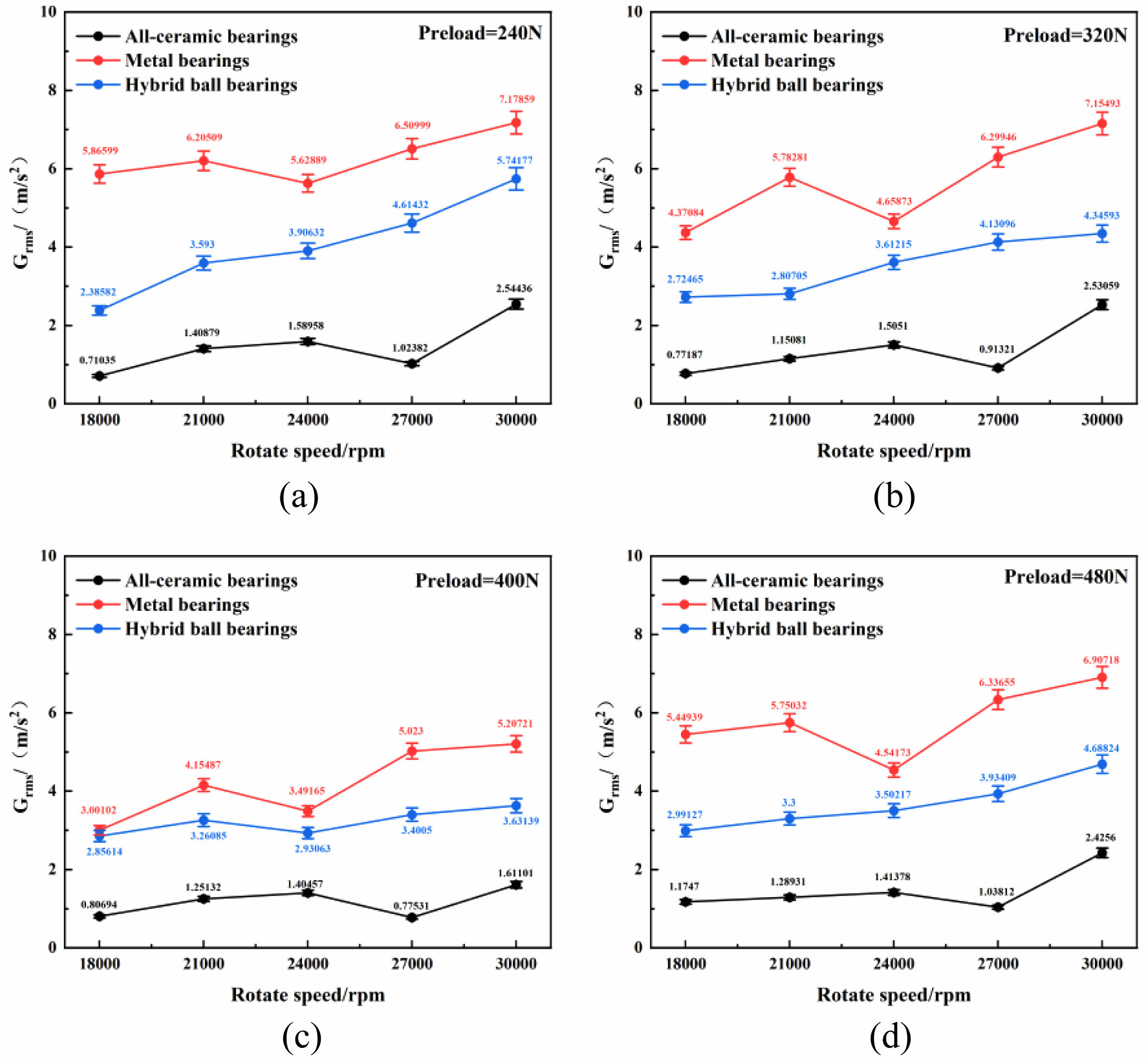
Higher rotational speeds amplify centrifugal forces on bearing balls, increasing vibration amplitudes. Generally speaking, ceramic bearings have greater radial stiffness than traditional steel bearings, so the critical speed of full-ceramic bearings is greater than that of steel bearings While bearing vibration typically escalates with speed, Fig. 7 reveals distinct attenuation zones: metal bearings show vibration reduction at 24,000 rpm, whereas full-ceramic bearings achieve attenuation at 27,000 rpm. This phenomenon occurs when operational frequencies approach critical speeds. For the full-ceramic bearings, when the critical speed of the rotor system is within the range of critical speed, the phase angle lag occurs, which is exacerbated by the high damping characteristics of ceramic materials. The unbalanced excitation force vector is weakened through the self cancellation mechanism, resulting in the decrease of vibration value. In addition, the lipophilicity of ceramic materials will promote the formation of oil film, and its lubrication state transition is relatively gentle. For the metal bearings, when the rotating speed reaches 24,000 rpm, the phase lag of vibration response suddenly increases, resulting in nearly opposite excitation force and vibration speed vector, forming a transient dynamic balance. In addition, at a specific speed, the lubrication state inside the bearing will change from boundary lubrication to mixed lubrication, the minimum oil film thickness will increase, and the contact stiffness will decrease, leading to the decrease of vibration.
Among all bearing types, full-ceramic bearings exhibit the least vibration, as seen in Fig. 7. At 18,000 rpm, the minimum RMS value is 0.71035 m/s² under a 240 N preload, while at 21,000 rpm, the minimum RMS value is 1.15081 m/s² under a 320 N preload. As the speed increases to 24,000-30,000 rpm, the gyroscopic rotation of the balls intensifies, requiring a higher preload to mitigate its effects. At these speeds, the minimum RMS values are 1.40457 m/s², 0.77531 m/s² and 1.61101 m/s² under a 400 N preload. This suggests that an appropriate preload effectively constrains the gyroscopic motion of the balls, and the resulting contact deformation is insufficient to induce significant vibration. Moreover, at 30,000 rpm, the RMS value increases to 2.4256 m/s² and 2.53059 m/s² under 480 N and 320 N preloads, respectively. This indicates that both insufficient and excessive preload can lead to increased vibration. An inadequate preload fails to restrict the balls, while an excessive preload causes excessive contact deformation.
The ball material in hybrid bearings is identical to that of full-ceramic bearings, leading to similar gyroscopic rotation under comparable conditions. However, due to the superior hardness of ceramic compared to metal, the contact deformation between the raceways and balls is more pronounced in hybrid bearings, leading to increased vibrations. For hybrid bearings, the optimal preload varies with speeds, similar to full-ceramic bearings. The material properties of the metal balls produce greater gyroscopic torque and contact deformation compared to ceramic balls, making metal bearings exhibit the highest vibration levels among the three types. For metal bearings, as the preload rises, the vibration initially diminishes but then rises again. For instance, at 18,000 rpm, the RMS value is 3.00102 m/s² under a 400 N preload, but it increases to 5.44939 m/s² and 4.37048 m/s² under 480 N and 320 N preload. As the speed increases further, the vibration under a 400 N preload always remains minimal. This indicates that the experimental speed is relatively high for the metal bearings; higher preload leads to greater contact deformation and smaller preload is not enough to restrict balls, resulting in the vibration levels rising.
Impact of speed and preload on rotation frequency amplitude
The RMS comparison reveals that full-ceramic bearings exhibit the lowest vibration across various operating conditions. The impact of varying speeds and preload levels on the rotation frequency of full-ceramic bearings is discussed. The rotation frequency is calculated using the following formula:



where f_r represents the bearing's rotation frequency, and n denotes the spindle velocity.
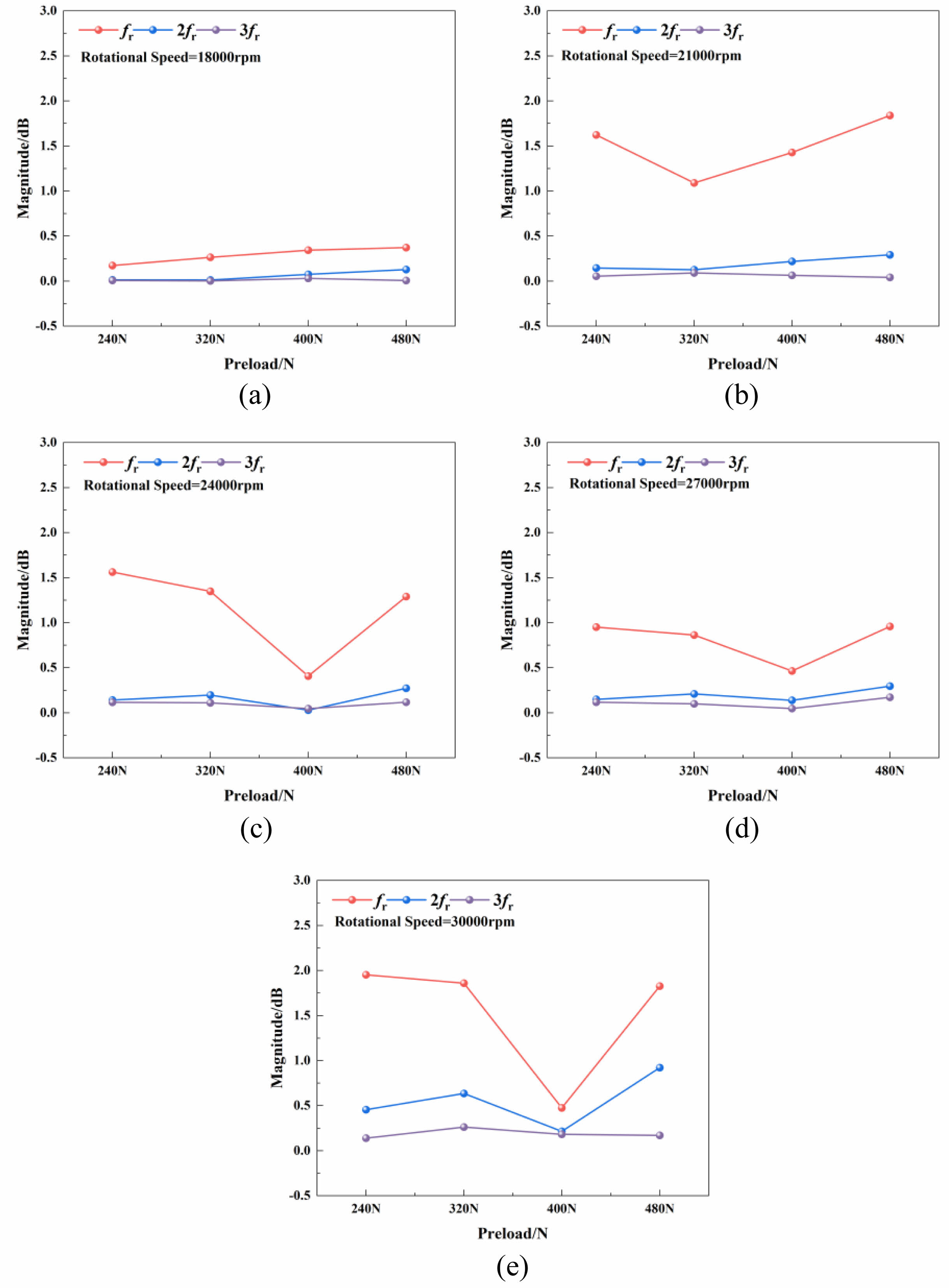
The bearing's operational state is evaluated by examining the rotational frequency and its harmonics across different situations, as shown in Fig. 8. The bearing's rotational frequency (f_r) is directly correlated with speed, and its contribution to vibration is paramount compared to its harmonics. As preload increases, f_r tends to rise at lower speeds. At elevated speeds, f_r initially decreases, and finally rises again. An increase in harmonics at f_r, especially a surge in 2f_r, often signifies that the poor bearing performance, characterized by a deterioration in neutrality and balance.
As shown in Fig. 8(a) and Fig. 8(b), at their respective speeds, the frequencies f_r and 2f_r reached the minimum values at preload of 240 N and 320 N, respectively. Both f_r and 2f_r increase when the preload increases and decreases. This indicates that these preload levels reach the better performance of the full-ceramic bearing. However, further increasing the preload significantly affects the bearing's neutrality, while insufficient preload may not adequately minimize the internal clearance, potentially affecting the bearing's performance and leading to an increase in both f_r and 2f_r frequencies. At higher speeds, as depicted in Figs. 8(c), 8(d), and 8(e), both f_r and 2f_r reached their minimum values at a preload of 400N. This suggests that a higher preload is necessary to enhance bearing stability at elevated rotating speeds. However, excessive preload can degrade the alignment between the inner and outer rings of the bearing, leading to an increase in f_r and 2f_r. For instance, as shown in Fig. 8(e), f_r rises significantly when the preload increases from 400 N to 480 N. Meanwhile, the 3f_r remains relatively small with minimal variation, similar to the behavior of 2f_r. These results underscore the critical role of precise preload in bearing design and operation. An optimal preload ensures stability and performance, while insufficient or excessive preload can compromise the bearing's neutrality and lead to instability.
Impact of speed and preload on temperature rise characteristics
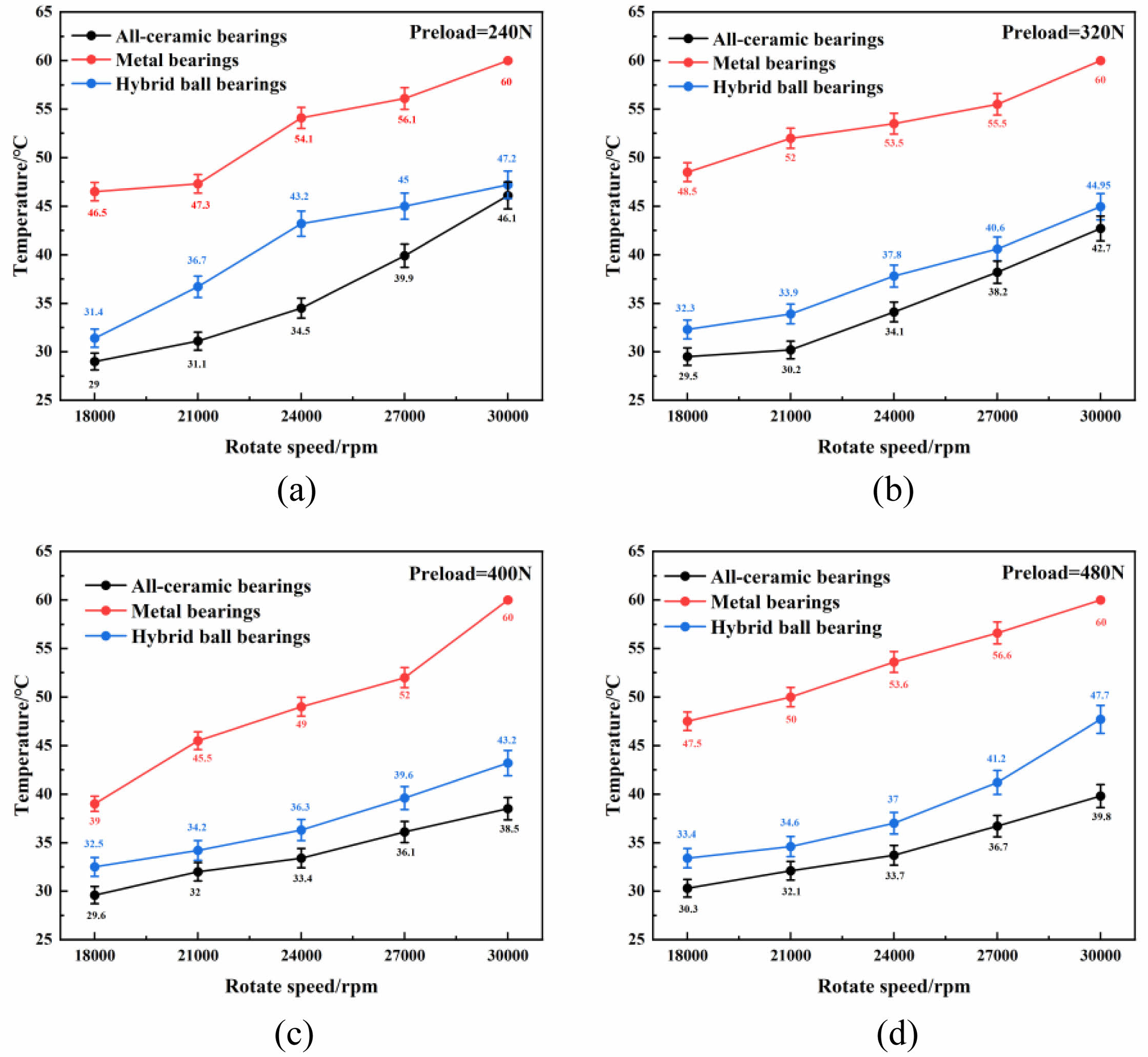
The steady-state temperature of bearings rises progre­ssively with speed, as seen in Fig. 9, under different preload levels. During the experiment, the metal bearing failed to stabilize at a steady-state when its speed attained 30,000 rpm, temperature beyond the 60 ℃ limit established by the experimental apparatus. Comparing the steady-state temperatures of three bearing types, metal bearings consistently exhibit the highest temperature. At 27,000 rpm, the metal bearing's temperature ranges from 52 ℃ to 56.5 ℃ under different preload levels, with the smallest temperature rise observed at a preload of 400 N. At 30,000 rpm, the hybrid bearing's temperature ranges from 45 ℃ to 47.7 ℃, with the smallest temperature rise observed at a preload of 400 N. Among the three types of bearings, the full-ceramic bearings achieve the lowest steady-state temperature. At 30,000 rpm, their temperature ranges from 38.5 ℃ to 46.1 ℃, with the smallest temperature rise observed at a preload of 400 N.
For full-ceramic bearings, at 18,000 rpm, the steady-state temperature increases with preload, reaching a maximum of 29 ℃ under 240 N. At this speed, the ball's spin motion is minimal, and a low preload (240 N) is sufficient to maintain optimal performance. However, higher preload elevates the contact load the ball with the raceway rises, leading to increased heat generation. At 21,000 rpm, the minimal temperature is 30.2 ℃ under 320 N. At 24,000 rpm or higher, a preload of 400 N achieves the lowest temperature rise. Here, the ball’s rotational action becomes more significant, and a lower preload fails to adequately restrict spin motion, increasing heat generation. Conversely, excessive preload significantly increases the contact stress between the ball and the raceway, further raising the temperature. For instance, at 30,000 rpm, the temperature is 38.5 ℃ at under 400 N, when the preload increases or decreases to 480 N or 320 N, but increases to 39.8 ℃ and 42.7 ℃ at 480 N and 320 N, respectively. For hybrid bearings, the temperature trend is similar to that of full-ceramic bearings, with the ideal preload varying depending on the speed. For metal bearings, due to the material properties of the metal ball, a higher preload is required at 18,000 rpm to restrict its spin motion. This results that in the smallest overall temperature rise at a preload of 400 N under different speeds.
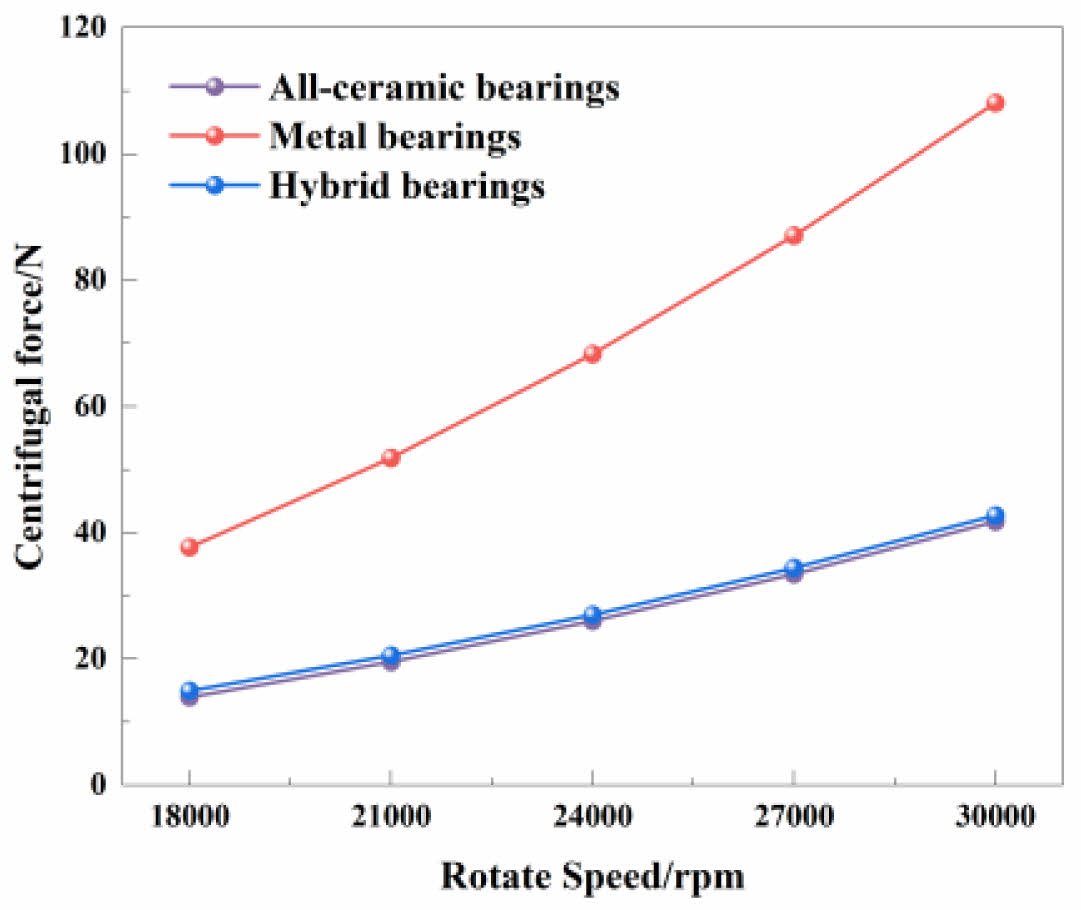
As shown in Fig. 10, the comparative analysis demonstrates that the ceramic ball exhibits significantly lower centrifugal force (reduced by approximately 38-65%) compared to metal ball, which is directly attributable to the lower density of ceramic material (3.2 g/cm³ vs. 7.81 g/cm³ for GCr15). This reduction in centrifugal force leads to a corresponding decrease in frictional force, resulting in lower temperature for full-ceramic and hybrid bearings compared to metal bearings. Additionally, the coefficient of friction for Si₃N₄-Si₃N₄ interfaces was found to be lower than that of GCr15-Si₃N₄. This friction coefficient disparity accounts for the 3-9 ℃ temperature elevation observed in hybrid bearings compared to full-ceramic bearings. In short, the exorbitant temperature of the metal bearing makes them unsuitable for high-speed applications (>18,000 rpm). In contrast, the full-ceramic bearings exhibit minimal temperature rise under various situations, making them more suitable for high-speed applications.

Through experimental analysis of full-ceramic, metal, and hybrid bearings under varying operational conditions, this study examines the effects of speeds and preload levels on dynamic and thermal characteristics. Key findings combine the pseudo-static data analysis and reveal three principal conclusions:
(1) Both speed and preload demonstrate significant influence on spin-roll ratio, contact load and deformation. The effect magnitude exhibits progressive amplification with increasing speed and preload, with preload playing a more dominant role than speed. Notably, the influence of speed on them decreases with the increase of preload.
(2) Test outcomes suggest that full - ceramic bearings are superior to the other bearing types in terms of temperature increase and vibration. At 27,000 rpm, the temperature of full-ceramic bearings is diminished by 30.1% relative to metal bearings, and vibration is decreased by 84.6% compared to the motorized spindle utilizing metal bearings. At 30,000 rpm, the temperature of full-ceramic bearings is diminished by 10.9% relative to hybrid bearings, and the vibration is decreased by 55.6% compared to the motorized spindle utilizing hybrid bearings.
(3) The impact of preload on full-ceramic and hybrid bearings shows a similar trend, which necessitates preload is roughly 240 N and 320 N, respectively, under 18,000 rpm and 21,000 rpm. As speed escalates, the requisite optimum preload correspondingly amplifies. At 24,000 rpm and further, the ideal preload for full-ceramic and hybrid bearings is around 400 N. In addition, for metal bearings, demand consistently a preload of 400 N across tested speeds due to material effects and restricted maximum speed.
Experimental research has shown that full-ceramic bearings display superior temperature rise and vibration performance. In comparison to conventional metal bearings, particularly under extreme operational conditions (18,000-30,000 rpm), full-ceramic bearings are more appropriate for motorized spindles. These findings provide empirical tests for adopting ceramic bearings in high-speed motorized spindle designs.

The authors would like to acknowledge the support of the Key Projects of the National Natural Science Foundation of China (joint fund) [grant number U23A20631], the National Key R&D Program [grant number 2024YFB3410202], the National Natural Science Foundation of China [grant number 52405123], the Liaoning Province's key industrial innovation task "Unveil the leader" project by the Liaoning Gongxin Investment [2023]177.